Journal of Comprehensive Pure and Applied Mathematics Volume 2 (2024), Article ID: CPAM-109
https://doi.org/10.33790/cpam1100109Research Article
A quotient of Fomin-Kirillov algebra and \(Q\)-Lucas polynomial
Sirous Homayouni
*Department of Mathematics, DePauw University, USA
Corresponding Author Details: Sirous Homayouni, Department of Mathematics, DePauw University, USA.
Received date: 10th August, 2024
Accepted date: 27th August, 2024
Published date: 29th August, 2024
Citation: Homayouni, S. (2024). A quotient of Fomin-Kirillov algebra and Q-Lucas polynomial. J Comp Pure Appl Math, 2(1): 109.
Copyright: ©2024, This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Abstract
We introduce a quotient of the Fomin-Kirillov algebra \(FK(n)\) denoted by \(\overline{FK}_{C_n}(n)\), over the ideal generated by the edges of a complete graph on \(n\) vertices that are missing in the \(n\)-cycle graph \(C_n\). In this quotient algebra, we establish a one-to-one correspondence between the basis elements and the set of matchings in an \(n\)-cycle graph. We prove that the Hilbert series of \(\overline{FK}_{C_n}(n)\) corresponds to the \(q\)-Lucas polynomials, and the dimension of this quotient algebra is equal to the Lucas number \(L_n\). We also find the character map of this quotient algebra over the Dihedral group \(D_n\).
Keywords: Lucas polynomial, Gröbner basis, ideal, quotient algebra, Hilbert series, ncycle graph.Motivation and Preliminaries
Fomin-Kirillov algebra \(FK(n)\) is a quadratic non-commutative algebra on generators \(x_{ij}=-x_{ji}\), where \(1\leq i<j\leq n\), that satisfy the following relations [6]. \[\label{rel} \begin{split} (i) : x_{ij}^2=0,~1\leq i < j \leq n;\\ (ii) : x_{ij}x_{kl} - x_{kl}x_{ij} = 0;~\text{for distinct}~ i, j, k, l~ \text{such that}~1\leq i, j, k<l \leq n;\\ (iii) : x_{ij}x_{jk} - x_{jk}x_{ik} - x_{ik}x_{ij} = 0; ~\text{if}~ 1\leq i < j < k\leq n;\\ (iii^\prime) : x_{ij}x_{ik} - x_{jk}x_{ij} + x_{ik}x_{jk} = 0; ~\text{if}~ 1\leq i < j < k\leq n. \end{split}----(1.1)\] If \(F\langle x_{ij}\rangle\) is the free associated algebra generated by \(x_{ij},~1\leq i<j\leq n\), then \(FK(n)\) is the quotient of \(F\langle x_{ij}\rangle\) over the ideal generated by the relations in (1.1).
While Fomin and Kirillov initially introduced this algebra with the
motivation of calculating the structure constants of Schubert
polynomials, it later garnered significant attention in both algebraic
and combinatorial contexts [1-3, 7-10]
The analysis of subalgebras within the Fomin-Kirillov algebra has
enhanced our understanding of this algebra, revealing a remarkable
structural similarity to Coxeter groups and their nil-Coxeter algebras
[3].
Despite extensive research on various aspects of this algebra, numerous questions remain unanswered. One such question pertains to its dimensionality. While the dimension of \(FK(n)\) is known to be finite for \(n=3,4,5\), it remains uncertain whether it is finite or not for \(n\geq 6\), [1, 3]
In this paper, to better understand the structure of \(FK(n)\) we study a quotient of it denoted
\(\overline{FK}_{C_n}(n)\) associated
with the subgraph \(n\)-cycle \(C_n\) of the complete graph on \(n\) vertices. While \(FK(n)\) is associated to the complete graph
on \(n\) vertices, \(\overline{FK}_{C_n}(n)\) is associated with
the subgraph \(n\)-cycle \(C_n\) of the complete graph on \(n\) vertices. We find a beautiful
connection between this quotient algebra and the theory of Lucas
polynomials. Specifically we find that the Hilbert series of this
quotient algebra is the \(q\)-Lucas
polynomial, and its dimension equals the Lucas number, as well the
symmetry properties of this quotient algebra under \(D_n\) is related to \(q\)-Fibonacci polynomials.
How much of the Fomin-Kirillov algebra and its unsolved questions can be explained or understood in terms of number theory? I hope my present work serves as an introduction toward my future research addressing this question.
1.1. Gröbner basis
In this paper, we focus on the generating set for the defining ideal of the algebra, which is a Gröbner basis. According to non-commutative Buchberger theory [11], the reduced Gröbner basis is unique up to monomial ordering. The monomial ordering we employ in this work is known as graded lexicographic ordering (glex). Here is how it is defined:
Definition 1.1. For monomials \(M_1\) and \(M_2\) we say \[M_1<_{glex}M_2~ \text{if}~\begin{cases} deg M_1<deg M_2, ~\text{or}\\ deg M_1=deg M_2~\text{and}~M_1<_{lex}M_2, \end{cases}\] where the lexicographic ordering (lex) of monomials is introduced by first establishing a variable ordering:
\[x_{ij} > x_{kl}~ \text{if}~ \begin{cases} j < l, ~\text{or}\\ j = l ~\text{and}~ i > k,\end{cases}.\] With this variable ordering, the following rule completes the definition of our lexicographic monomial ordering: For monomials \(M_1\) and \(M_2\) of the same usual degree \(d\), we have:
\(M_1 <_{lex} M_2\), if the first variable of \(M_1\) is less than the first variable of \(M_2\).
If the first \(k\) variables happen to be the same, then compare the \((k+1)\) st variables
A quotient algebra of
We introduce the algebra \(\overline{FK}_{C_n}(n)\) as the quotient of \(FK(n)\) by the ideal generated by the edges of the complete graph on \(n\) vertexes that are missing in the subgraph \(n\)-cycle \(C_n\). In other words, we define \(\overline{FK}_{C_n}(n)\) as following: \[\begin{split} \overline{FK}_{C_n}(n)=& \frac{FK(n)}{I\langle\text{missing edges in subgraph}~ C_n\rangle} \\=& \frac{F\langle x_{ij}\rangle}{I\langle \{\text{generators of the defining ideal of $FK(n)$}\}\cup \{\text{missing edges in}~C_ n\}\rangle}. \end{split}\]Here, \(FK(n)\) represents an algebra with generators \(\{x_{ij}\}\) and \(I\langle \text{missing edges in subgraph} C_n\rangle\) denote the ideal generated by the missing edges in the subgraph \(C_n\). In other words by putting the missing edges in (1.1) equal to zero we come up with the new set of relations (2.1) associated to \(\overline{FK}_{C_n}(n)\) as in the following definition.
Definition 2.1. For \(n>3\), we define \(\overline{FK}_{C_n}(n)\), the quotient algebra of \(FK(n)\), as the algebra on generators \(\{x_{1n}=-x_{n1},~x_{m,m+1}=-x_{m+1,m}, 1\leq m\leq n-1\}\), that satisfies the following relations (Leading terms are underlined). \[\label{2terms} \begin{split} R_{C_n}=&\{ x_{m,m+1}^2=0,~1\leq m\leq n-1,~ x_{1,n}^2=0, \\& x_{m,m+1}x_{m+1, m+2}=0, ~x_{m+1,m+2}x_{m,m+1}=0,~ 1\leq m \leq n-2,\\& x_{n-1,n}x_{1n}=0,~x_{1n}x_{n-1,n}=0,~x_{12}x_{1n}=0,~x_{1n}x_{12}=0,\\&\underline{x_{m,m+1}x_{l,l+1}}-x_{l,l+1}x_{m,m+1}=0, ~1\leq m\leq l-2,~ 3\leq l\leq n-1,\\& \underline{x_{m,m+1}x_{1,n}}-x_{1n}x_{m,m+1}=0,~ 2\leq m\leq n-2\}. \end{split}----(2.1)\]
From the relations in (2.1) we have the following set of generators for the defining ideal of \(\overline{FK}_{C_n}(n)\). \[\label{2terms''} \begin{split} &\textbf{\text{Generators of defining ideal of}}~ \overline{FK}_{C_n}(n)=\\&\{ x_{m,m+1}^2,~1\leq m\leq n-1,~ x_{1,n}^2, \\& x_{m,m+1}x_{m+1, m+2}, ~x_{m+1,m+2}x_{m,m+1},~ 1\leq m \leq n-2,\\& x_{n-1,n}x_{1n},~x_{1n}x_{n-1,n},~x_{12}x_{1n},~x_{1n}x_{12},\\&\underline{x_{m,m+1}x_{l,l+1}}-x_{l,l+1}x_{m,m+1}, ~1\leq m\leq l-2,~ 3\leq l\leq n-1,\\& \underline{x_{m,m+1}x_{1,n}}-x_{1n}x_{m,m+1},~ 2\leq m\leq n-2\}. \end{split}\]
Remark 2.2. As mentioned earlier, the generators of \(FK(n)\) correspond to the edges of a complete graph on \(n\) vertices. In contrast, the generators of \(\overline{FK}_{C_n}(n)\) are specifically the edges of the subgraph \(C_n\) within the complete graph on \(n\) vertices. These generators are denoted as \(\{x_{12}, x_{23}, \cdots,x_{n-1,n},x_{1n}\}\). Now let’s discuss the action of permutation group on this algebra.
\(S_n\) and \(FK(n)\): The symmetric group naturally defines an action on \(FK(n)\). This action arises because the defining ideal of \(FK(n)\) remains stable under the permutations in \(S_n\). However when we consider \(\overline{FK}_{C_n}(n)\), the situation changes.
\(S_n\) and \(\overline{FK}_{C_n}(n)\): The defining ideal of \(\overline{FK}_{C_n}(n)\) is generated by the terms listed in (2.2). This ideal is not stable under the action of \(S_n\). for instance, consider the term \(x_{12}^2\) from (2.2). Under the transformation \((1n)\in S_n\), goes into \(X_{2n}^2\), which is not part of the original set of generators.
\(D_n\) and \(\overline{FK}_{C_n}(n)\): However there is a silver lining! The ideal defining \(\overline{FK}_{C_n}(n)\) is stable under the action of dihedral group \(D_n\). Consequently, \(D_n\) defines a valid action on \(\overline{FK}_{C_n}(n)\). An action can be defined on a quotient algebra if and only if the defining ideal remains stable under that action.
2.1. Dihedral group.
Dihedral group is defined by \[D_n=\langle r, s|s^2=1, r^n=1, (rs)^2=1\rangle.\] We realize group \(D_n\) in the permutation group \(S_n\), where \[\label{r,s}\begin{split} r=(12\cdots n)~\text{and}~s&=\begin{cases} (1, n)(2, n-1)\cdots (\frac{n}{2}, \frac{n}{2}+1), & \text{even}~n,\\ (1, n)(2, n-1)\cdots (\frac{n-1}{2}, \frac{n+3}{2})(\frac{n+1}{2}), & \text{odd}~n, \end{cases} \end{split}----(2.3)\] are permutations on \(n\) vertexes (rotation and reflections in \(C_n\), see Figure 1.
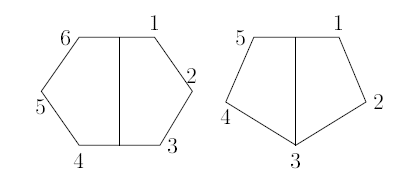
Figure: 1 Examples of reflections s in an n-cycle for even and odd n. s = (16)(25)(34) in a 6-cycle and s = (15)(24)(3) in a 5-cycle.
2.2. The stability of the defining ideal of \(\overline{FK}_{C_n}(n)\) under \(D_n\)
It is easily shown that the set of generators of the defining ideal of \(\overline{FK}_{C_n}(n)\) in (2.2) is invariant under \(D_n\). So the defining ideal of \(\overline{FK}_{C_n}(n)\) is stable under \(D_n\). Therefore \(D_n\) defines an action on \(\overline{FK}_{C_n}(n)\).
2.3. The action of \(D_n\) on \(\overline{FK}_{C_n}(n)\)
We define the action of \(D_n\) realized as a permutation group, on \(\overline{FK}_{C_n}(n)\) as: \[\label{d_n-def} D_n:\overline{FK}_{C_n}(n)\to \overline{FK}_{C_n}(n) ~\text{by}~ \sigma(M+I)\mapsto \sigma M+I,----(2.4)\]where the action of \(\sigma\in D_n\) on a monomial \(M\), is defined via its action on a variable \(x_{ij}\) (where \(j=i+1\)), representing an edge of an \(n\)-cycle, by: \[\label{sigmax} \sigma x_{ij}=\begin{cases} x_{\sigma(i)\sigma(j)}~&\text{if}~ \sigma(i)<\sigma(j),\\ -x_{\sigma(j)\sigma(i)}~&\text{otherwise}, \end{cases}----(2.5)\] and multiplicative extension of it to monomial \(M\).
The algebra is closed under \(D_n\) as the defining ideal is stable under \(D_n\). Regarding the action defined in (2.4), we need to check the following items.
Well-defined: \[\begin{split} &M+I= M'+I\to M-M'\in I\to \sigma(M-M')\in I \text{ (as $I$ is stable under $D_n$)}.\\ &\text{Then}~\sigma M-\sigma M'\in I \to \sigma M+I=\sigma M'+I\to \sigma(M+I)=\sigma(M'+I). \end{split}\]
Identity axiom: \(\epsilon(f(x_{i_1j_1},\cdots,x_{i_kj_k})+I)=f(x_{i_1j_1},\cdots,x_{i_kj_k})+I\),
Compatibility axiom: \[\begin{split} (\sigma_1\sigma_2)(f(x_{i_1j_1},\cdots,x_{i_kj_k})+I)=&f((\sigma_1\sigma_2)x_{i_1j_1},\cdots, (\sigma_1\sigma_2)x_{i_kj_k})+I\\=&f(x_{(\sigma_1\sigma_2)i_1(\sigma_1\sigma_2)j_1},\cdots, x_{(\sigma_1\sigma_2)i_k(\sigma_1\sigma_2)j_k})+I\\=&f(x_{\sigma_1(\sigma_2i_1)\sigma_1(\sigma_2j_1)},\cdots, x_{\sigma_1(\sigma_2i_k)\sigma_1(\sigma_2j_k})+I\\=&\sigma_1f(x_{\sigma_2i_1\sigma_2j_1},\cdots, x_{\sigma_2i_k\sigma_2j_k})+I\\= & \sigma_1(\sigma_2f(x_{i_1j_1},\cdots, x_{i_kj_k}))+I. \end{split}\]
Hence the map in (2.4), defines an action on \(\overline{FK}_{C_n}(n).\)
2.4. Representation decomposition of \(\overline{FK}_{C_n}(n)\)
Usual degree decomposition: The action of \(D_n\) on \(\overline{FK}_{C_n}(n)\) defined in (2.4) permutes the indexes among themselves but does not change the number of variables in a monomial. Therefore usual degree remains invariant under \(D_n\). Therefore, the usual degree representation decomposition makes sense for \(\overline{FK}_{C_n}(n)\) (i.e., \(D_n\) respects decomposition in usual degree). \[\label{oplus1} \overline{FK}_{C_n}(n)=\bigoplus_{d\geq 0} \overline{FK}_{C_n}^{(d)}(n).----(2.6)\]
Conjugacy class decomposition: \(S_n\)-degree is well defined on \(\overline{FK}_{C_n}(n)\), since the generators of the defining ideal in (2.2) are homogeneous with respect to \(S_n\). The action of \(D_n\) on \(\overline{FK}_{C_n}(n)\) defined in (2.4) does not change the cycle type of the \(S_n\)-degrees assigned to elements of \(\overline{FK}_{C_n}(n)\). The reason is that a monomial of degree \(\sigma\), when acted upon by a permutation \(\nu\), is sent to a monomial of degree \(\nu^{-1}\sigma\nu\) which is a conjugate of \(\sigma\) by definition of conjugacy. So permutation \(\nu\) sends \(\sigma\) to a conjugate of \(\sigma\), i.e., conjugacy class is invariant under \(D_n\) realized in permutation group. Hence the conjugacy class decomposition is a representation decomposition: \[\label{oplus} \overline{FK}_{C_n}(n)=\bigoplus_{\mu} \overline{FK}_{C_n}^{\mu}(n),----(2.7)\]where \(\overline{FK}_{C_n}^{\mu}(n)\) stands for all the elements of \(S_n\)-degree \(\sigma\) in \(\overline{FK}_{C_n}(n)\) that belong to the conjugacy class indexed by \(\mu\).
Remark 2.3. Every permutation \(\sigma\) can be expressed using only transpositions \((1,2)\), \((2,3),\cdots (n-1,n)\). As a result, has the potential to be non-zero for any permutation \(\sigma\). However, in our special cases( as discussed in sections 3.1 and 3.3), we observe that for many permutations, \(\overline{FK}_{C_n}^{\sigma}(n)\) evaluates to zero. Having an \(S_n\)-conjugacy class does not necessarily imply that it is also a \(D_n\)-conjugacy class. For instance, consider the transpositions \((2,3)\) and \((2,5)\) within the same \(S_n\)-conjugacy class (for n>5). These transpositions are not conjugated via an element in \(D_n\). However, in section (2.6), we will explore a very special basis (2.15). From this basis, we find that any two elements in an \(S_n\) conjugacy class can be conjugated via a rotation or reflection in \(D_n\) realized in permutation group. Consequently, an \(S_n\) conjugacy class is also a \(D_n\) conjugacy class. Due to the reasons mentioned above, we cannot further refine (2.7).
Set-partition type decomposition:
a) Set-partition degree and Homogeneous Generators: Set-partition degree is well-defined on \(\overline{FK}_{C_n}(n)\), since the generators of the defining ideal in (2.2) exhibit homogeneity with respect to set-partition degree. For any monomial \(M\) in \(\overline{FK}_{C_n}(n)\), the appearance of \(x_{ij}\) implies that indices \(i\) and \(j\) belong to the same part of the set-partition degree.
b) Action of \(D_n\) on Monomials: Consider an \(x_{ij}\) appearing in \(M\). Under the action of \(\sigma \in D_n\) (as definition in (2.5)) it transforms to \(x_{\sigma(i)\sigma(j)}\) if \(\sigma(i)<\sigma(j)\), and to \(-x_{\sigma(j)\sigma(i)}\) otherwise. As a result of the action, the indexes \(\sigma(i)\) and \(\sigma(j)\) now belong to the same part of the set-partition degree. While the action of \(D_n\) rearranges indices within a part, it does not alter the number of indices in that part. In other words, the set-partition type remains invariant under the action of \(D_n\) realized in the permutation group. We can express \(\overline{FK}_{C_n}(n)\) as a direct sum over set-partition types: \[\label{oplus1} \overline{FK}_{C_n}(n)=\bigoplus_{\phi} \overline{FK}_{C_n}^{\phi}(n),\] where \(\overline{FK}_{C_n}^{\phi}(n)\) represents all elements of set-partition degree \(\lambda\) belonging to the same set-partition type indexed by \(\phi\).
Remark 2.4<\b>. Unlike permutations (as discussed in Remark (2.3), not every set-partition can be obtained by joining only consecutive entries modulo \(n\). For example, it is not possible to obtain the set-partition \(\{\{1,3\},\{2\}, \{4\}\}\). Consecutively, for certain set-partitions denoted as \(A\), the space \(\overline{FK}_{C_n}^{A}(n)\) evaluates to zero. Later in section 2.6, we will explore our very special basis (2.15) for which, for any two non-zero \(\overline{FK}_{C_n}^{A}(n)\) and \(\overline{FK}_{C_n}^{B}(n)\), where \(A\) and \(B\) have same partition type, we can find an element of \(D_n\) that maps \(A\) into \(B\). Consequently, a class of the same set-partition type can be a \(D_n\) conjugacy class. Due to the reasons mentioned above, we cannot refine (2.8)
2.5. Gröbner basis
Degree-\(2\) terms: From the non-commutative Buchberger theory [11], the set of generators of the defining ideal of \(\overline{FK}_{C_n}(n)\) in (2.2) establish the degree \(2\) elements of the Gröbner basis.
Degree-\(3\) terms: To find the degree-\(3\) terms, we need to reduce the \(S\)-polynomials between any two pairs of degree-\(2\) terms with respect to lower degree terms.
We observe that the \(S\)-polynomial between two monomials is always zero. Moreover, the only \(S\)-polynomials that reduce to non-zero elements for Gröbner basis are:
\(S(\underline{x_{m,m+1}x_{1n}}-x_{1n}x_{m,m+1}, x_{1n}x_{12}, 3)\),
\(S(\underline{x_{1,n}x_{12}}, x_{m,m+1}x_{l,l+1}-x_{l,l+1}x_{m,m+1}, 3)\).
Item \(1\) reduces to: \[A=\{ x_{1n}x_{m,m+1}x_{12},~ 3\leq m\leq n-2\},\] The range of \(m\) is due to the fact that if \(m\) is less than or equal to \(2\), it would be divisible by the relation \(x_{m+1,m+2}x_{m,m+1}=0, (\text{for}~1\leq m \leq n-2\)) when \(m=1\).
Item \(2\) reduces to: \[B=\{x_{1n}x_{l,l+1}x_{12},~ 3\leq l\leq n-2\}.\] The range of \(l\) ensures that \(x_{1n}x_{l,l+1}x_{12}\) is not divisible by the relation \(x_{1n}x_{n-1,n}=0\).Interestingly, sets \(A\) and \(B\) are the same. Since the set of degree-\(3\) elements in relations of \(\overline{FK}_{C_n}(n)\) is empty, the following set constitutes the entire degree-\(3\) Gröbner basis: \[\label{3terms} \text{degree-$3$ terms}: \{x_{1n}x_{m,m+1}x_{12}: ~ 3\leq m\leq n-2\}.----(2.9)\]
Example 2.5. For \(n=4\), there are no degree-\(3\) terms.
For \(n=5\), the only degree-\(3\) term in the Gröbner basis is \(x_{15}x_{34}x_{12}\).
For \(n=6\), there are two degree-\(3\) terms: \(x_{16}x_{34}x_{12}\) and \(x_{16}x_{45}x_{12}\).Degree-\(4\) terms: To find degree-\(4\) terms, we only need to consider one \(S\)-polynomial (since the rest vanish): \[S(\underline{x_{m_2,m_2+1}x_{1n}}-x_{1n}x_{m_2,m_2+1},x_{1n}x_{m_1,m_1+1}x_{12},4).\] This \(S\)-polynomial, with respect to terms of degree less than \(4\), reduces to: \[x_{1n}x_{m_2,m_2+1}x_{m_1,m_1+1}x_{12},\] However, these terms reduce to zero unless the following inequalities hold: \[m_2-m_1\geq 2, ~~~m_1\geq 3,~~~ m_2\leq n-2.\] The terms \(x_{1n}x_{m_2,m_2+1}x_{m_1,m_1+1}x_{12}\) constitute the only degree-\(4\) terms, as the set of elements of degree \(4\) in the relations of \(\overline{FK}_{C_n}(n)\) is empty. Therefore, we have: \[\label{4terms}\text{\textbf{Degree-$4$ terms}}: \{x_{1n}x_{m_2,m_2+1}x_{m_1,m_1+1}x_{12}:~ m_2-m_1\geq 2,~m_1\geq 3 ~\text{and} ~m_2\leq n-2\}.----(2.10)\]
The terms of degrees \(3\) and \(4\) in Equations (2.9) and (2.10) provide insights into a general form for the elements of degree \(k\geq 4\) in the basis of \(\overline{FK}_{C_n}(n)\). Let’s explore this further with the following proposition:
Proposition 2.6. For \(k\geq 4\), any degree-\(k\) element of Gröbner basis for the ideal associated with \(\overline{FK}_{C_n}(n)\) is of the form: \[\label{kterms} \begin{split} &x_{1n}x_{m_{k-2}m_{k-2}+1}x_{m_{k-3}m_{k-3}+1} \cdots x_{m_2m_2+1}x_{m_1m_1+1}x_{12},~ \text{where},\\& m_{i}-m_{i-1}\geq 2,~i=2, 3, \cdots, k-2, ~\text{and}~ ~m_1\geq 3 ~\text{and} ~m_{k-2}\leq n-2. \end{split}----(2.11)\]
Proof. (by induction)
Base of induction: Equation (2.10) for \(k=4\) serves as the base of induction.
Inductive step: Assume that the statement is valid for degree-\(k\) elements of the Gröbner basis. We need to show that it is valid for degree-\((k+1)\) elements. Specifically, we want to prove that for degree-\((k+1)\) elements, we have: \[\label{kterms''} \begin{split} x_{1n}x_{m_{k-1}m_{k-1}+1}x_{m_{k-2}m_{k-2}+1}x_{m_{k-3}m_{k-3}+1} \cdots x_{m_2m_2+1}x_{m_1m_1+1}x_{12},~\text{where}\\m_i-m_{i-1}\geq 2,~i=2, 3, \cdots, k-1, ~\text{and}~ ~m_1\geq 3 ~\text{and} ~m_{k-1}\leq n-2. \end{split}----(2.12)\] However, the only \(S\)-polynomials available between a degree-\(k\) element in the statement and a lower degree term, which could reduce to a degree-\((k+1)\) element of the Gröbner basis is (as the rest vanish), are given by: \[\label{1}\begin{split}S(x_{m_{k-1}m_{k-1}+1}x_{1n}-x_{1n}x_{m, m+1},~ x_{1n}x_{m_{k-2}m_{k-2}+1}x_{m_{k-3}m_{k-3}+1} \cdots x_{m_1m_1+1}x_{12},~ k+1)\\=x_{1n}\underline{x_{m_{k-1}m_{k-1}+1}x_{m_{k-2}m_{k-2}+1}} \cdots x_{m_1m_1+1}x_{12}. \end{split}----(2.13)\] We now focus on the underlined product on the right hand side of (2.13): \[C=\underline{x_{m_{k-1},m_{k-1}+1}x_{m_{k-2},m_{k-2}+1}}.\] To ensure that \(C\) does not vanish or reduce to something else when reduced with any of the degree-\(2\) terms in (2.1), we need to avoid the following cases.
If \(m_{k-1}=m_{k-2}\) then \(C\to 0\) due to the relation \(x_{m,m+1}^2=0\).
If \(m_{k-1}=m_{k-2}-1\), then \(C\to 0\) due to the relation \(x_{m,m+1}x_{m+1,m+2}=0\).
If \(m_{k-1}\leq m_{k-2}-2\), then \(C\to x_{m_{k-2}m_{k-2}+1}x_{m_{k-1}m_{k-1}+1}\) (by reduction with the leading term of the relation \(\underline{x_{m,m+1}x_{l,l+1}}-x_{l,l+1}x_{m,m+1}=0)\)
If \(m_{k-1}\leq m_{k-2}+1\), then \(C\to 0\) by the relation \(x_{m+1,m+2}x_{m,m+1}=0\).
To avoid these cases, we require the inequality \(n-2\geq m_{k-1}>m_{k-2}+1\), which is equivalent to \(m_{k-1}-m_{k-2}\geq 2\). Additionally, we need \(m_1\ge 3\) to ensure that \(x_{m_1,m_{m_1+1}x_{12}}\) does not become zero due to \(x_{m+1, m+2}x_{m,m+1}=0\) for \(1\le m\le n-2.\)
Therefore the following three inequalities meet the requirement of (2.12) for validity at degree \(k+1\): \[m_{k-1}-m_{k-2}\geq 2,~ n-2\geq m_{k-1},~ \text{and}~m_1\geq 3.\]
This completes the proof. ◻
By combining the degree-\(k\) terms for \(k\geq 4\) from (2.11), the degree-\(3\) term from (2.9) and the degree-\(2\) terms from (2.1), we obtain the Gröbner basis \(GB_{\overline{FK}_{C_n}(n)}\) for the ideal associated with \(\overline{FK}_{C_n}(n)\): \[\label{gb'} \begin{split} GB_{\overline{FK}_{C_n}(n)}=&\{x_{m,m+1}^2:~1\leq m\leq n-1; ~x_{1,n}^2,\\& x_{m,m+1}x_{m+1, m+2}, ~x_{m+1,m+2}x_{m,m+1}, ~1\leq m \leq n-2\\&x_{n-1,n}x_{1n}, ~x_{1n}x_{n-1,n},~x_{12}x_{1n},~x_{1n}x_{12}\\&x_{m,m+1}x_{l,l+1}-x_{l,l+1}x_{m,m+1}, ~1\leq m\leq l-2,~ 3\leq l\leq n-1\\& x_{m,m+1}x_{1,n}-x_{1n}x_{m,m+1},~ 2\leq m\leq n-2,\\& x_{1n}x_{m,m+1}x_{12}, ~ 3\leq m\leq n-2,~\text{and}\\& x_{1n}x_{m_{k-2}m_{k-2}+1}x_{m_{k-3}m_{k-3}+1} \cdots x_{m_2m_2+1}x_{m_1m_1+1}x_{12},\\&\text{where}~ m_i-m_{i-1}\geq 2,~i=2, 3, \cdots, k-1, ~\text{and}~ ~m_1\geq 3 ~\text{and} ~m_{k-1}\leq n-2\}. \end{split}----(2.14)\]
Example 2.7. For \(n=3\) we have \[GB_{\overline{FK}_{C_3}(3)}=\{x_{12}^2,x_{23}^2,x_{13}^2, x_{12}x_{23}, x_{23}x_{13}, x_{12}x_{13}, x_{23}x_{12}, x_{13}x_{23}, x_{13}x_{12}\}.\]
2.6. Basis and dimension
Definition 2.8.
A matching in a graph is a subset of the set of edges in the graph where no two edges share a common vertex.
A matching on a set of line segments \(V_n=\{\overline{12},\overline{23},\cdots \overline{n-1,n}\}\) is a subset of \(V_n\) where no two line segments have a common vertex.
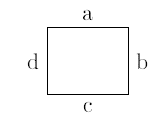
Example 2.9. Consider a square with successive sides/edges labelled as \(a, b, c,\text{and} ~d\). We have \(7\) sets of sides/edges where no two of them share a common vertex: \[\phi, \{a\}, \{b\}, \{c\}, \{d\}, \{a,c\}, \{b,d\}.\] Therefore, the number of matchings in a square is \(7\).
Theorem 2.10
There exists a one-to-one correspondence between the basis of \(\overline{FK}_{C_n}(n)\) and the set of matchings in an \(n\)-cycle \(C_n\).
The dimensions of \(\overline{FK}_{C_n}(n)\) equals the number of matchings in an \(n\)-cycle \(C_n\).
Proof. The basis of the algebra \(\overline{FK}_{C_n}(n)\) consists of all
the words formed from generators
\(\{x_{12},x_{23},x_{34},\cdots,
x_{n-1,n}; x_{1,n}\}\) that are not divisible by any
leading term of the elements in the Gröbner basis from (2.14). Specifically:
The element of degree \(0\) is \(1\),
The elements of degree \(1\) are the generators \(x_{1n}\) and \(x_{m,m+1},\text{for} ~m=1, \cdots, n-1\).
However, for higher degree terms in \(\overline{FK}_{C_n}(n)\), the structure of the degree-\(2\) terms and higher degree terms in the Gröbner basis from (2.14) leads to the following observations:
Any monomial formed from our generators vanish due to the degree-\(2\) terms in the Gröbner basis if it has two adjacent \(1\)st indices differing by \(\pm{1}\) or \(0\).
Any monomial formed from our generators vanishes if two adjacent \(1\)st indices differ by more than or equal to \(2\) but are increasing in \(1\)st indices.
If any two adjacent \(2\)nd indices in a monomial share the common value \(n\), then the monomial vanishes by \(x_{n-1,n}x_{1n}\).
If any two adjacent \(2\)nd indexes share a common value less than \(n\), then since all the generators are of the form \(x_{m,m+1}\), they also share a common 1st index, leading to vanishing by \(x_{ij}x_{ij}\).
To avoid the above \(4\) cases, the basis elements of \(\overline{FK}_{C_n}(n)\) must consist of monomials in variables with decreasing \(1\)st indices (with the exception of \(x_{1n}\) when appears as the leading variable), such that any two successive \(1\)st indices differ by at least \(2\).
Considering the above points we come up with \(B(\overline{FK}_{C_n}(n))\), the basis of
\(\overline{FK}_{C_n}(n)\): \[\label{b}
\begin{split}
B&(\overline{FK}_{C_n}(n))=\{1,~x_{1n},~x_{m,m+1},~\text{where}~
1\leq m \leq n-1,\\&
x_{1n}x_{m_1m_1+1},~~\text{where}~ 2\leq m_1 \leq
n-2,\\&x_{m_1m_1+1}x_{m_2m_2+1}, ~\text{where}~m_1-m_2\geq
2,~m_2\geq1,~m_1\leq n-1,
\\&x_{m_1m_1+1}x_{m_2m_2+1}\cdots
x_{m_km_k+1},~\text{where}~
m_i-m_{i+1}\geq 2,~m_k\geq 1,~m_1\leq n-1,
\\&
x_{1n}x_{m_1m_1+1}x_{m_2m_2+1} \cdots
x_{m_{k-1}m_{k-1}+1}, ~\text{where}~
m_i-m_{i+1}\geq 2,~ m_{k-1}\geq 2,\\&m_1\leq n-2
\}.
\end{split}----(2.15)\] Consider the algebra \(\overline{FK}_{C_n}(n)\) and its basis
\(B[\overline{FK}_{C_n}(n)]\), we want
to show that this basis consists of all the matchings in the \(n\)-cycle graph \(C_n\).
Viewing Variables as Edges:
In the basis of \(\overline{FK}_{C_n}(n)\) given in (2.15), let’s interpret the variables \(x_{m,m+1}\) for \(m=1, 2, \cdots, n-1\) and \(x_{1n}\), as representing the edges \(\overline{12}, \overline{23},\cdots \overline{n-1,n}\) and \(\overline{1n}\) of the \(n\)-cycle \(C_n\). Each element in the basis corresponds to a subset of the edges of \(C_n\).
Matching Interpretation: An element in the basis of \(\overline{FK}_{C_n}(n)\) can be viewed as a matching in the graph \(C_n\). The reason is that no monomial in the basis includes two variables with a common index. Therefore, we can view an element of the basis as a subset of the set of \(C_n\) edges with no common vertex. Hence, an element of the basis corresponds to a subset of the edges of \(C_n\) with no common vertex, which is precisely the definition of a matching.
Converse Interpretation: Conversely, any matching in \(C_n\) can be represented as an element in the basis of \(\overline{FK}_{C_n}(n)\). Furthermore, considering the domain of the indexes in (2.15), we see that all the monomials in the generators of \(\overline{FK}_{C_n}(n)\) that have no repeated indices are covered in the basis.
one-to-on correspondence, and the dimension of \(\overline{FK}_{C_n}(n)\): The above considerations establish a one-to-one correspondence between the set of all matchings in the \(n\)-cycle \(C_n\) and the basis of \(\overline{FK}_{C_n}(n)\). Therefore the dimension of algebra \(\overline{FK}_{C_n}(n)\) is equal to the number of matching in the \(n\)-cycle \(C_n\).
This completes the proof. ◻
Corollary 2.11. The dimension of \(\overline{FK}_{C_n}(n)\) is equal to the Lucas number \(L_n\).
Proof. From Theorem 2.10 we know that the dimensions of \(\overline{FK}_{C_n}(n)\) correspond to the number of matchings in an \(n\)-cycle \(C_n\), which precisely equals the Lucas number \(L_n\) [13]. This completes the proof. ◻
2.7. The highest degree elements in the basis
Consider the basis of \(\overline{FK}_{C_n}(n)\) as given in (2.15). We want to find the maximum degree of a monomial in the basis, which corresponds to the maximum size of a matching. This maximum degree occurs when any two adjacent 1st indices differ by exactly \(2\) (equivalently, when any two sides in the corresponding matching are separated by exactly one side in \(C_n\)).
We can calculate this maximum degree as follows:
\[\label{maxdeg}\begin{split}\text{For}~n\geq 4, ~ \text{the maximum degree/size}~= \lfloor\frac{n}{2}\rfloor,\\ \text{The multiplicity of the maximum degree/size}~=\begin{cases} 2, &\text{for even}~n\\ n, &\text{for odd}~n \end{cases} \end{split}----(2.16)\]
Example 2.12. For \(n=5\), the highest degree for elements in \(B[\overline{FK}(5)]\) is \(\lfloor\frac{n}{2}\rfloor=\lfloor\frac{5}{2}\rfloor=2\), and its multiplicity \(5\).
2.8. Matchings’ and Fibonacci number
The following Lemma establishes the connection of Fibonacci number to the number of matching in a set of line segments.
Lemma 2.13. Let \(M(n)\) denote the number of matchings in
the set of line segments
\(V_n=\{\overline{12},\overline{23},\cdots
\overline{n-1,n}\}\), \(n\geq
2\). Then \[\label{chi5'}
M(n)=F_n,~ n\geq 2,----(2.17)\] where \(F_n\) is \(n\)-th Fibonacci number with initial values
\(F_0=1,~F_1=1\).
Proof. We need to show that:
\(M(2)=F_2\), and
\(M(n+1)=M(n)+M(n-1)\), i.e., the recurrence relation for Fibonacci numbers , .
Base Case: For \(n=2\) the set \(V_2=\{\overline{12}\}\) contains two subsets: the empty set \(\phi\), and itself \(\{\overline{12}\}\). Thus \(M(2)=2\), which matches the Fibonacci number \(F(2)=2\) (with initial values \(F_0=1\) and \(F_1=1\)).
Inductive Step: Consider \(V_n\) as a union: \[V_n=\{\overline{n-1, n}\}\cup V_{n-1},~ \text{where}~ V_{n-1}=\{\overline{12},\overline{23},\cdots\overline{n-2, n-1}\}.\] Adding a line segment \(\overline{n,n+1}\) to \(V_n\) creates the set \(V_{n+1}\). This addition increases \(M(n)\), the number of matchings in \(V_n\), by introducing new matchings. To avoid common vertices, we add \(\overline{n,n+1}\) only to each matching in \(V_{n-1}\). Note that \(\overline{n,n+1}\) shares no common vertex with elements in \(V_{n-1}\) but does share a common vertex \(n\) with \(\overline{n-1,n}\). Therefore the number of new matchings added to \(M(n)\) is precisely the number of matchings in \(V_{n-1}\), which is \(M(n-1)\). Thus we have \(M(n+1)=M(n)+M(n-1)\). This completes the proof.
◻
Lemma 2.14. Let \(M(n,k)\) denote the number of matchings of size \(k\) in the set of line segments \(V_n=\{\overline{12},\overline{23},\cdots \overline{n-1,n}\}\). Then
\(M(n+1,k)=M(n,k)+M(n-1,k-1), ~\text{for}~ n\geq 2,~k\geq 0\),
\(M(n, k)={n-k\choose k}\).
Proof.
Consider \(V_n\) as \[V_n=V_{n-1}\cup \{\overline{n-1,n}\},\] where \(V_{n-1}=\{\overline{12},\overline{23},\cdots \overline{n-2,n-1}\}\). Addition of the line segment \(\overline{n,n+1}\) to \(V_n\) makes \[V_{n+1}=\{\overline{n,n+1}\}\cup V_{n-1}\cup \{\overline{n-1,n}\}.\] This addition increases \(M(n, k)\). To avoid common vertices, we add \(\overline{n,n+1}\), as before, only to each matching in \(V_{n-1}\). The reason is that \(\overline{n,n+1}\) does not share a common vertex with elements in \(V_{n-1}\) but have a common vertex \(n\) the elements in \(\{\overline{n,n+1}\}\) and \(\{\overline{n-1,n}\}\). So the number of the new matchings is exactly the number of elements in \(V_{n-1}\) of size \(k-1\), i.e., \(M(n-1, k-1)\). Hence we have: \[M(n+1,k)=M(n,k)+M(n-1,k-1).\]
To prove \(M(n, k)={n-k\choose k}\) we use double induction. We need to show that
Base Case: For \(n=2\) and \(k=1\) the statement \(M(2,1)={2-1\choose 1}\) is true, as \(M(2,1)=1\) and \({2-1\choose 1}={1\choose 1}=1\).
Inductive Step: We need to show that \[\begin{split} \text{If}~ &M(n,k)={n-k\choose k} \forall n\geq 2,~k>1,~\text{then}~ M(n+1,k)={n+1-k\choose k},\\ \text{and}\\ \text{If}~ &M(n,k)={n-k\choose k} \forall n\geq 2,~k>1,~\text{then}~ M(n,k+1)={n-(k+1)\choose k+1}. \end{split}\] By part (1) of the Lemma we have: \[\begin{split} M(n+1,k)&=M(n, k)+M(n-1, k-1)\\&={n-k\choose k}+{n-1-(k-1)\choose k-1}={n-k\choose k}+{n-k\choose k-1}\\ &=\frac{(n-k)!}{k!(n-2k)!}+\frac{(n-k)!}{(k-1)!(n-2k+1)!}=\cdots=\frac{(n-k+1)!}{k!(n-2k+1)!}\\&={n+1-k\choose k}.\\ \text{Also,}\\ % \text{if}~ &M(n,k)={n-k\choose k} \forall n\geq 2,~k>1,~\text{then}~ M(n,k+1)={n-k-1\choose k+1}.\\ M(n,k+1)&=M(n-1, k+1)+M(n-2, k)\\&={n-1-(k+1)\choose k+1}+{n-2-k\choose k}={n-k-2\choose k+1}+{n-k-2\choose k}\\ &=\frac{(n-k-2)!}{(k+1)!(n-2k-3)!}+\frac{(n-k-2)!}{k!(n-2k-2)!}=\cdots=\frac{(n-k-1)!}{(k+1)!(n-2k-21)!}\\&={n-k-1\choose k+1}={n-(k+1)\choose k+1}. \end{split}\]
This completes the proof. ◻
The following proposition establishes the connection of the number of matchings in a set of line segments with that of an \(n\)-cycle graph \(C_n\).
Proposition 2.15. . Consider an \(n\)-cycle graph denoted \(C_n\). Let \(M_{C_n}(n,k)\) represent the number of matchings of size \(k\) in \(C_n\). Additionally, let \(M(n, k)\) be the number of matchings of size \(k\) in the set of line segments \(V_n=\{\overline{12},\overline{23},\cdots \overline{n-1,n}\}\). Then we have: \[\label{123'} \begin{split} M_{C_n}(n, k)=&M(n, k)+M(n-2, k-1),~n\geq 4, ~k=2, 3, \cdots, \lfloor\frac{n}{2}\rfloor,~and\\ &M_{C_n}(n, k)=\frac{n}{n-k}{n-k\choose k}, \end{split}----(2.18)\]
Proof. \(M(n, k)\) could be viewed as the number of matchings of size \(k\) in \(C_n\setminus{\{\overline {1n}\}}\). We rewrite \(C_n\setminus{\{\overline {1n}\}}\) as \[C_n\setminus{\{\overline {1n}\}}=\{\overline{12} \}\cup V_{n-2}\cup \{\overline{n-1,n}\},\] where \(V_{n-2}=\{\overline{23},\overline{34}, \cdots, \overline{n-2,n-1}\}\). Now adding \(\overline{1n}\) to \(C_n\setminus{\{\overline {1n}\}}\) completes the \(n\)-cycle, as well increases \(M(n, k)\) to \(M_{C_n}(n, k)\) by making new matchings of size \(k\). As before, to avoid common vertices we need to add the edge \(\overline{1n}\) to the elements of size \(k-1\) only in \(V_{n-2}\).
Therefore, the number of the new matchings equals the number of
matchings of size \(k-1\) in \(V_{n-2}\), that is, \(M(n-2, k-1)\). Hence, we have \(M_{C_n}(n, k)=M(n, k)+M(n-2, k-1)\). This
completes the proof of the first part.
To prove the second part, we substitute \(M(n,
k)={n-k\choose k}\) from Lemma 15 into the first
part, as follows. \[\begin{aligned}
\begin{split}
M_{C_n}(n, k)&=M(n, k)+M(n-2, k-1)={n-k\choose
k}+{n-1-k\choose k-1}\\&={n-k\choose
k}+\frac{(n-1-k)!}{(k-1)!(n-2k)!}={n-k\choose
k}+\frac{\frac{(n-k)!}{(n-k)}}{\frac{k!}{k}(n-2k)!}\\&={n-k\choose
k}+\frac{k}{n-k}\frac{(n-k)!}{k!(n-2k)!}={n-k\choose
k}+\frac{k}{n-k}{n-k\choose k}\\&=\frac{n}{n-k}{n-k\choose k}.
\end{split}
\end{aligned}----(2.19)\] This completes the proof. ◻
2.9. Hilbert series and \(q\)-Fibonacci/\(q\)-Lucas polynomials
[4, 5]. Putting together Proposition 2.15, Theorem 2.10, Corollary 2.11, and equation (2.16), we obtain: \[L_n=M_{C_n}(n)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}M_{C_n}(n,k)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}\frac{n}{n-k}{n-k\choose k}.\] The upper limit in the sum is due to the fact that maximum size of a matching in \(C_n\) or the maximum degree of an element in the basis of \(\overline{FK}_{C_n}(n)\) is \(\lfloor\frac{n}{2}\rfloor\).
Hence taking sum over all the matchings of different size \(k\) in \(C_n\) (elements of different degrees \(k\) in the basis, we have \(q\)-Lucas polynomial [4, 5]: \[\label{q-lucas} L_n(q)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}\frac{n}{n-k}{n-k\choose k}q^k,~L_0=2.----(2.20)\] From Lemmas 2.13 and 2.14 we have the total number of matchings in a set of line segments \(V_n=\{\overline{12},\overline{23},\cdots \overline{n-1,n}\}\) to be \(M_n=F_n\) and the number of matchings of size \(k\) in \(V_n\) to be \(M(n,k)={n-k\choose k}\). This results in \[F_n=M(n)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}M(n,k)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}{n-k\choose k}.\] Hence taking sum over all matchings of different sizes we have \(q\)-Fibonacci polynomial [4, 5]: \[\label{q-fibo} F_n(q)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}{n-k\choose k}q^k.----(2.21)\] Considering the information above, we can establish a connection between the \(q\)-Lucas polynomial and the Hilbert series of \(\overline{FK}_{C_n}(n)\) in the following proposition:
Proposition 2.16. The Hilbert series of \(\overline{FK}_{C_n}(n)\) is given by the \(q\)-Lucas number \(L_n(q)\): \[H_n(q)=L_n(q).----(2.22)\]
Proof. Recall the expression for the \(q\)-Lucas number from Equation (2.20): \[L_n(q)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}\frac{n}{n-k}{n-k\choose k}q^k,~L_0=2.\] In the above expression, the degree \(k\), representing the size of the matching, is summed over to yield the Lucas number. By Corollary 2.11, this Lucas number is equal to the dimension of \(\overline{FK}_{C_n}(n)\). Thus, the expression demonstrates that the Hilbert series is indeed given by Lucas \(q\)-number: \[H_n(q)=\sum_{k=0}^{\lfloor\frac{n}{2}\rfloor}\frac{n}{n-k}{n-k\choose k}q^k=L_n(q).\] This completes the proof. ◻
Example 2.17. \(H_5(q)=\sum_{k=0}^{\lfloor \frac{5}{2}\rfloor}\frac{5}{5-k}{5-k\choose k}q^k= %{5\choose 0}+\frac{5}{4}{4\choose 1}q+\frac{5}{3}{3\choose 2}q^2= 1+5q+5q^2\). Similarly \(H_6=1+6q+9q^2+2q^3\).
2.10. The action of \(D_n\) and decomposition
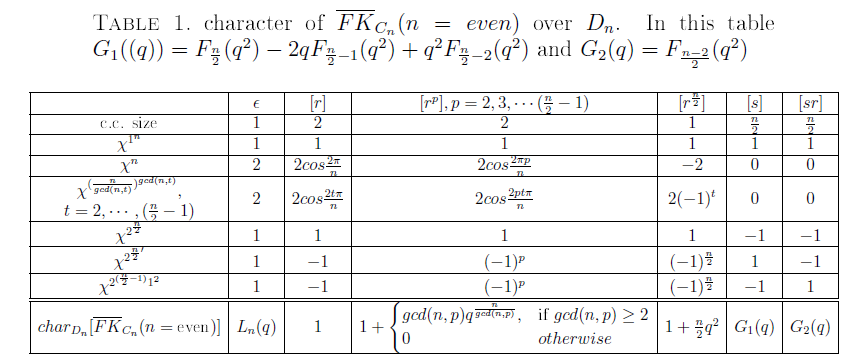
In this section we derive the character of \(\overline{FK}_{C_n}(n)\) over \(D_n\) for even and odd \(n\).
Remark 2.18. As previously mentioned, \(D_n\) defines an action on the algebra \(\overline{FK}_{C_n}(n)\). Under this action, the component of the character of \(\overline{FK}_{C_n}(n)\) associated with the conjugacy class indexed by \(\sigma\in D_n\) is the sum of the coefficients of \(z\) in \(\sigma(z)\) when \(z\) runs through the basis \(B[\overline{FK}_{C_n}(n)]\).
Lemma 2.19. Let \(r\in D_n\) realized in permutation group \(S_n\) as \(r=(1,2,\cdots,n)\). Then the trace of the representation of \(r^p\in D_n\), on \(\overline{FK}_{C_n}(n)\) is given by: \[\label{r^p} [\chi(r^p)](q)=\begin{cases} 1 ~$if$~ p=1\\ 1+\begin{cases} gcd(n,p)q^\frac{n}{gcd(n, p)},\text{if} ~~ 2\le p\le n-1,\text{and} ~ gcd(n, p)\ge\begin{cases} 2,~ n=\text{even}\\ 3,~n=\text{odd} \end{cases}\\ 0 ~~~~~~~~~~\text{otherwise} \end{cases}\\ H_n(q), \text{Hilbert series}, ~~~~~\text{if} ~~ p=n \end{cases}----(2.23)\]
Proof. In the following discussion, we consider \(M\) both as a basis element of \(\overline{FK}_{C_n}(n)\) and as a matching in \(C_n\). Similarly we treat \(r\) alternatively as a clockwise rotation of angle \(\frac{2\pi}{n}\) in \(C_n\) or as an operator acting on \(M\) as an eigenvector in \(r^pM=M\) with eigenvalue \(1\).
We consider the following points.
For any integer \(1\le p\le n\), there always exists an empty matching (equivalently, the identity element \(M=1\) in the basis), such that \(r^pM=M\).
\(rM=M\) does not hold for non-empty \(M\). The reason is that since \(r\) represents a clockwise rotation of \(\frac{2\pi}{n}\) in \(C_n\), it takes an edge in the matching \(M\) to the neighbouring edge in \(C_n\). However this neighbouring edge is not part of \(M\), as it could violate the definition of a matching (which forbids common vertices). Thus, \(rM=M\) cannot hold for a non-empty matching \(M\) (or any basis element \(M\neq 1\)). In other word, \(r^pM=M\) is ruled out for \(p=1\) and non-empty matchings.
The possibility of \(r^pM=-M\) is absurd. If we consider \(x_{m, m+1}\) as a general variable in a basis element \(M\), where \(1\leq m< n\), then for \(1< p\le n-1\) (since \(p=1\) is ruled out), we have: \[r^px_{m,m+1}=x_{(m+p)(mod~ n), (m+1+p)(mod~ n)}.\] We focus on the indices of \(x_{(m+p)(mod~ n), (m+1+p)(mod~ n)}\) and examine the following possibilities:
\((m+p)(mod~n)\le n-1\), then \((m+1+p) (mod~n)\le n.\) Then\[r^px_{m,m+1}=x_{(m+p)(mod~n),(m+1+p)(mod~n))}=x_{m', m'+1}~\] where \(m'=(m+p)(mod~n)\le n-1\).
No negative sign develops in this case. Therefore we are left with the following case:\((m+p)(mod~n)=n\), then \((m+1+p)(mod~n)=1.\) We have: \[r^px_{m,m+1}=x_{(m+p)(mod~n),(m+1+p)(mod~n))}=x_{n, 1}=-x_{1,n}.\] Here, a minus sign does develop. However, for \(r^pM=-M\) to hold, we would require that \(r^px_{1,n}=x_{m',m'+1}\) for some \(m'\) (to compensate for the \(x_{1n}\) generated by the operation of \(r^p\) on \(M\)). But then \[r^px_{1,n}=x_{1+p, (n+p)(mod~n)}=x_{1+p, p}=-x_{p,p+1}.\] Here, a second minus sign cancels out the first one. Therefore \(r^pM=-M\) is absurd. This is why \(gcd(n, p)\) was mentioned in the statement of the Lemma, as the number of eigenvectors \(M\).
The second item above rules out \(p=1\) in the equation \(r^pM=M\) for nonempty matching \(M\).
For \(r^pM=M\) to hold, we require that the matching \(M\) be periodic with period \(p\). In fact, a matching can be periodic with period \(gcd(n, p)\) and still be fixed by \(r^p\). Specifically, a matching \(M\) in \(C_n\), after a clockwise rotation of \(gcd(n, p)\), coincides itself. Therefore the number of edges in \(M\) is \(\frac{n}{gcd(n, p)}\), and the number of such matchings \(M\) equals \(gcd(n,p)\). Alternatively, we can express this as the number of non-identity elements in the basis of degree \(\frac{n}{gcd(n, p)}\), that are fixed by \(r^p\), which equals \(gcd(n,p)\). Thus, we can write the character as \(gcd(n,p)q^{\frac{n}{gcd(n,p)}}\), where, we also include the identity element(empty matching) that is always fixed.However, [maxdeg], imposes a restriction on the highest degree: \[\frac{n}{gcd(n, p)}\le \lfloor\frac{n}{2}\rfloor\]or equivalently: \[\begin{cases} gcd(n,p)\ge 2,~ \text{for even}~ n\\ gcd(n,p)\ge \frac{2n}{n-1},~ \text{for odd}~n \end{cases}\] Since \(\frac{2n}{n-1}>2\) for finite \(n\), and \(gcd(n,p)\) is a natural number, we have \(\frac{2n}{n-1}\ge 3\). Therefore, the above restriction is modified as follows: \[\begin{cases} gcd(n,p)\ge 2,~ \text{for even}~ n\\ gcd(n,p)\ge 3,~ \text{for odd}~n \end{cases}\]
putting everything together, we obtain the following expression for the character: \[\label{char11'''''} \chi(r^p)= 1+\begin{cases} gcd(n,p)q^\frac{n}{gcd(n, p)},&\text{if} ~~ 2\le p\le n-1,\text{and} ~ gcd(n, p)\ge\begin{cases} 2,~ n=\text{even}\\ 3,~n=\text{odd} \end{cases}\\ 0 ~~~~~~~~~~&\text{otherwise} \end{cases}----(2.24)\]
For \(p=n\), where \(r^p=r^n=\epsilon\), represents the identity element of \(D_n\), we have \(\chi(r^n=\epsilon)= dim[\overline{FK}_{C_n}(n)]=L_n\) by corollary 12. Alternatively, in the degree decomposition \(q\)-Lucas form, we express \(L_n(q)=H_n(q)\), which corresponds to the Hilbert series of \(\overline{FK}_{C_n}(n)\) according to Proposition 2.16. Therefore, the character of identity element of the group over the quotient algebra would be: \[\label{char11''''''} \chi(r^n=\epsilon)=L_n(q)=H_n(q)----(2.25)\]
The combination of the above items \(1-5\), along with Equations (2.24) and (2.25) provides the proof of the lemma. ◻
Example 2.20. Consider \(\overline{FK}_{C_6}(6)\). Then \[\begin{split}B[\overline{FK}_{C_n}(n)]=\{1, x_{12}, x_{23}, x_{34}, x_{45}, x_{56}, x_{16},\\ x_{34}x_{12}, x_{45}x_{12}, x_{45}x_{23}, x_{56}x_{12}, x_{56}x_{23}, x_{56}x_{34}, x_{16}x_{23}, x_{16}x_{34}, x_{16}x_{45},\\ x_{16}x_{45}x_{23}, x_{56}x_{34}x_{12}\}\end{split}\] Then, for \(2\le p\le 5\), such that \(\frac{6}{gcd(6,p)}\le \lfloor \frac{6}{2}\rfloor\) , i.e. \(gcd(6,p)\ge 2\), we will have the options \(p=2, 3, 4\). Therefore we will have:
\(\chi(r)=1\)
\(\chi(r^2)=3\) or \(\chi(r^2)(q)=1+2q^3\),
\(\chi(r^3)=4\) or \(\chi(r^3)(q)=1+3q^2\),
\(\chi(r^4)=3\) or \(\chi(r^4)(q)=1+2q^3\),
\(\chi(r^5)=1\)
\(\chi(r^6=\epsilon)=18\) or \(\chi(r^6)(q)=L_6(q)=H_6(q)=1+6q+9q^2+2q^3\).
Lemma 2.21. For even \(n\geq 4\), let \(s\in D_n\), be realized in permutation
group as
\(s=(1n)(2, n-1)\cdots (\frac{n}{2},
\frac{n}{2}+1)\) in an \(n\)-cycle graph \(C_n\). Let \(\chi(s)\) be the trace of the
representation of \(s\) over \(\overline{FK}_{C_n}(n)\). Then we have:
\[\label{char1}
[\chi(s)](q)=\sum_{k=0}^{\lfloor\frac{n}{4}\rfloor}{\frac{n}{2}-k\choose
k}q^{2k}-2\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose
k}q^{2k+1}+\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-2}{2}\rfloor}{\frac{n}{2}-2-k\choose
k}q^{2k+2}.----(2.26)\] In terms of \(q\)-Fibonacci polynomials, according to the
total degree decomposition we have: \[(q)=F_{\frac{n}{2}}(q^2)-2qF_{\frac{n}{2}-1}(q^2)
+q^2F_{\frac{n}{2}-2}(q^2),----(2.27)\]where \(F\) represents the appropriate \(q\)-Fibonacci polynomial.
Proof.
By Theorem 11 to any element of the basis of \(\overline{FK}_{C_n}(n)\) there corresponds a matching in \(C_n\). Let \(T_1=\{\overline{i_1,i_1+1}, \overline{i_2,i_2+1}\cdots \overline{i_m,i_m+1}\}\) be a matching of the set of line segments \(S_1=\{\overline{12}, \overline{23}, \cdots,\overline{\frac{n}{2}-1, \frac{n}{2}}\}\) in \(C_n\) as defined in Definition 9. It has a corresponding monomial: \[u=x_{i_1,i_1+1}x_{i_2,i_2+1}\cdots x_{i_m,i_m+1}\in B[\overline{FK}_{C_n}(n)].\] Now consider the reflection in \(s\) of the matching \(T_1\) ( and its corresponding monomial \(u\)), Since \(n\) is even, this reflection is itself a matching. let’s denote it as: \[T'_1=\{\overline{j_1,j_1+1}, \overline{j_2,j_2+1}\cdots \overline{j_m,j_m+1}\}.\]Also denote its corresponding monomial as: \[u'=x_{j_1j_1+1}x_{j_2j_2+1}\cdots x_{j_mj_m+1}.\]
While the matching \(T_1\) is not symmetric about \(s\), the union of the matchings \(T_1\cup T'_1\) is symmetric, and its corresponding monomial \(uu' \in B[\overline{FK}_{C_n}(n)]\) is invariant under \(s\). This can be seen as follows: \[s(uu')=s(usu)=(su)s^2u=(su)u=u'u \xrightarrow{\mbox{\tiny{reduction w.r.t degree-2 terms}}} uu'.\] The last step in the above equation involves reduction with respect to degree-\(2\) terms in the Gröbner basis (2.14), since \(u\) and \(u'\) commute (there are no common indices among variables in \(uu'\)). The number of such eigenvectors in \(\overline{FK}_{C_n}(n)\) equals the number of matchings \(T_1\cup T_1'\) in \(C_n\). By construction, this is equivalent to the number of matchings \(T_1\) in the set \(\{\overline{12}, \overline{23}, \cdots,\overline{\frac{n}{2}-1,\frac{n}{2}}\}\). Using Equations (2.17) and (2.21) we find that this number is equal to: \[\label{chi1'} [M(\frac{n}{2})](q)=F_\frac{n}{2}(q)=\sum_{k=0}^{\lfloor\frac{n}{4}\rfloor}{\frac{n}{2}-k\choose k}q^{k}.----(2.28)\] However, each matching in \(T_1\cup T_1'\) contains twice as many edges as \(T_1\) does.
Therefore, our first contribution to \(\chi(s)\), denoted as \(\chi_1(s)\) is given by: \[\label{chi1} [\chi_1^{}(s)](q)=\sum_{k=0}^{\lfloor\frac{n}{4}\rfloor}{\frac{n}{2}-k\choose k}q^{2k}=F_{\frac{n}{2}}(q^2).----(2.29)\] Next, to fine the number of eigenvectors with eigenvalue \(-1\) we consider the following cases:
We consider the matching \(\{\overline{1n}\}\cup T_2\), where \(T_2\subset\{\overline{23},\cdots, \overline{\frac{n}{2}-1,\frac{n}{2}}\}\). We denote the reflection of \(T_2\) in \(s\) as \(T_2'\). we also consider \(v\) and \(v'\) as the corresponding monomials in \(B[\overline{FK}_{C_n}(n)]\), for \(T_2\) and \(T_2'\), respectively.
We consider the matching \(\{\overline{\frac{n}{2}, \frac{n}{2}+1}\}\cup T_3\) where \(T_3\) is a matching in \(\{\overline{12},\cdots, \overline{\frac{n}{2}-2,\frac{n}{2}-1}\}\). We also consider its reflection \(T_3'\) in \(s\).
In case \(1\), while the matching \(\{\overline{1n}\}\cup T_2\) is not symmetric about \(s\), the union \(\{\overline{1n}\}\cup T_2\cup T_2'\) forms a matching in \(C_n\) that is symmetric about \(s\). The corresponding monomial \(x_{1n}vv'\) forms an eigenvector of \(s\) with eigenvalue \(-1\), because: \[s(x_{1n}vv')=-x_{1n}s(vv')=-x_{1n}vv'.\]
By construction, the number of matchings \(\{\overline{1n}\}\cup T_2\cup T_2'\) in \(C_n\) equals the number of matchings \(T_2\) in \(\{\overline{23},\cdots, \overline{\frac{n}{2}-1,\frac{n}{2}}\}\), which according to (2.17) and (2.21) is equal to: \[\label{chi2'} [M(\frac{n}{2}-1)](q)=F_{\frac{n}{2}-1}(q)=\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^{k}.----(2.30)\]
However, while the number of matchings \(T_2\) equals that of \(\{\overline{1n}\}\cup T_2\cup T_2'\), but the number of edges in each matching of \(\{\overline{1n}\}\cup T_2\cup T_2'\) is \(2k+1\) compared to \(k\) edges of \(T_2\). The odd number \(2k+1\), reflects the odd size of the matching \(\{\overline{1n}\}\cup T_2\cup T_2'\) in \(C_n\), as well the negative eigenvalue of \(s\). Therefore we have: \[-\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^{2k+1}= -qF_{\frac{n}{2}-1}(q^2).\]where the rearrangement of \(q\) on the right hand side of the equation is for the sake of consistency with to definition of \(q\)-Fibonacci. Also the negative sign in the above is due the negative eigenvalue of \(s\). Having this for the case \((1)\), and considering the fact that the case \((2)\) also gives exactly the same result as case \((1)\), we apply a factor \(2\) for the above and hence we come up with a second contribution to \(\chi(s)\): \[\label{chi2} [\chi_2^{}(s)](q)=-2\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^{2k+1}=-2qF_{\frac{n}{2}-1}(q^2).----(2.31)\]
To cover the last contribution to \(\chi(s)\), we consider the matching \[\{\overline{1n}\}\cup\{\frac{n}{2}, \frac{n}{2}+1\}\cup T_4\cup T'_4.\] Here \(T_4\) is a matching in \(\{\overline{23},\overline{34},\cdots, \overline{\frac{n}{2}-2,\frac{n}{2}-1}\}\) (to avoid developing common vertex with \(\overline{1n}\) or \(\overline{\frac{n}{2}, \frac{n}{2}+1}~)\) and \(T'_4\) its reflection in \(s\). We also consider \(w\) and \(w'\), which are the corresponding monomials to \(T_4\) and \(T_4'\), respectively.
By similar arguments as before, we have eigenvectors with eigenvalues \(+1\). The number of such eigenvectors equals the number of matchings \(T_4\subset\{\overline{23},\overline{34}, \cdots,\overline{\frac{n}{2}-2,\frac{n}{2}-1}\}\) which is given by Equations (2.17)and (2.21): \[\label{chi3'} [M(\frac{n}{2}-2)](q)=F_{\frac{n}{2}-2}(q)=\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-2}{2}\rfloor}{\frac{n}{2}-2-k\choose k}q^{k}.----(2.32)\] However, while the number of matchings \(T_4\) equals that of \(\{\overline{1n}\}\cup\{\frac{n}{2}, \frac{n}{2}+1\}\cup T_4\cup T'_4\), the number of edges in each matching of the latter is \(2k+2\) compared to \(k\) edges in \(T_4\).
Hence our last contribution to \(\chi(s)\) is \[\label{chi3} [\chi_3^{}(s)](q)=\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-2}{2}\rfloor}{\frac{n}{2}-2-k\choose k}q^{2k+2}=q^2F_{\frac{n}{2}-2}(q^2).----(2.33)\]
Now, adding up the contributions from Equations (2.29), (2.31) and (2.33) we arrive at: \[(q)=\sum_{k=0}^{\lfloor\frac{n}{4}\rfloor}{\frac{n}{2}-k\choose k}q^{2k}-2\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^{2k+1}+\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-2}{2}\rfloor}{\frac{n}{2}-2-k\choose k}q^{2k+2}.\] This expresion is written in the following \(q\)-Fibonacci form using (2.21): \[(q)=F_{\frac{n}{2}}(q^2)-2qF_{\frac{n}{2}-1}(q^2) +q^2F_{\frac{n}{2}-2}(q^2).\] This completes the proof. ◻
Example 2.22.. For \(n=6\) we have \([\chi(s)](q)=F_3(q^2)-2qF_2(q^2)
+q^2F_1(q^2)\).
Let \(q=1\), then \(\chi(s)\to F_3-2F_2+F_1=3-2(2)+1=0\).
Lemma 2.23.. For even \(n\), Let \(s,
r\in D_n\), be realized in permutation group \(S_n\) as
\(s=(1,n)(2, n-1)\cdots (\frac{n}{2},
\frac{n}{2}+1)\) and \(r=(1,2,\cdots,n)\), in an \(n\)-cycle graph \(C_n\). Then we have: \[\label{char3}
[\chi(sr)](q)=\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose
k}q^{2k}, ~n\geq 4,----(2.34)\] and in \(q\)-Fibonacci form according to total
degree decomposition, we have: \[(q)=F_{\frac{n}{2}-1}(q^2),~n\geq 4,----(2.35)\]
where \(\chi(sr)\) is the trace of the
representation of \(sr\) over \(\overline{FK}_{C_n}(n)\).
Proof. Considering \(s\) and \(r\) as defined in the statement we will have: \[sr=(1,n-1)(2,n-2)\cdots (\frac{n}{2}-1,\frac{n}{2}+1).\] Therefore the only matchings in the \(n\)-cycle \(C_n\), symmetric about \(sr\), are \(T\cup T'\), where \(T\) is a matching in \(\{\overline{12},\overline{23},\cdots, \overline{\frac{n}{2}-2,\frac{n}{2}-1}\}\) and \(T'\) its reflection in \(sr\). The corresponding monomials to \(T\) and \(T'\) are \(w\) and \(w'\), respectively.
we have eigenvectors of \(sr\) with eigenvalue \(+1\), as \(sr(ww')=ww'\) as before. The number of such eigenvectors equals the number of matchings \(T\cup T'\) in \(C_n\) which equals the number of matchings \(T\) in \(\{\overline{12},\overline{23},\cdots, \overline{\frac{n}{2}-2,\frac{n}{2}-1}\}\) which is by (2.17) and (2.21) equal to: \[(q)=M(\frac{n}{2}-1)(q)=F_{\frac{n}{2}-1}(q)=\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^k.\] However, while the number of matchings \(T\cup T'\) equals that of \(T\), but the number of edges in each matching \(T\cup T'\) is \(2k\) compared to the \(k\) edges of \(T\). Therefore we have: \[(q)=\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^{2k}=F_{\frac{n}{2}-1}(q^2).\] This completes the proof. ◻
Example 2.24. For \(n=6\), we have \(\chi(sr)=\sum_{k=0}^1{2-k\choose k}q^{2k}={2\choose 0}+{1\choose 1}q=1+q^2\).
Lemma 2.25. For odd \(n\), Let \(s\in
D_n\) realized in permutation group \(S_n\) as
\(s=(1,n)(2, n-1)\cdots (\frac{n-1}{2},
\frac{n+3}{2})(\frac{n+1}{2})\) in an \(n\)-cycle graph \(C_n\). Then \[\label{char2}
[\chi(s)](q)=\sum_{k=0}^{\lfloor\frac{n-1}{4}\rfloor}{\frac{n-1}{2}-k\choose
k}q^{2k}-\sum_{k=0}^{\lfloor\frac{n-3}{4}\rfloor}{\frac{n-3}{2}-k\choose
k}q^{2k+1},----(2.36)\] with the \(q\)-Fibonacci version: \[(q)=F_\frac{n-1}{2}(q^2)-qF_\frac{n-3}{2}(q^2),\]
where \(\chi(s)\) is the trace of the
representation of \(s\) over \(\overline{FK}_{C_n}(n)\).
Proof.
Consider a matching \(T_1\): \[T_1=\{\overline{i_1,i_1+1}, \overline{i_2,i_2+1}\cdots \overline{i_m,i_m+1}\}\] of the following set of line segments. \[S=\{\overline{12}, \overline{23}, \cdots,\overline{\frac{n-1}{2}-1, \frac{n-1}{2}}\}.\] where the corresponding monomial of \(S\) is: \[u=x_{i_1,i_1+1}x_{i_2,i_2+1}\cdots x_{i_m,i_m+1}.\] Let the reflection of \(T_1\) in \(s\), itself a matching, be \(T'_1\): \[T'_1=\{\overline{j_1,j_1+1}, \overline{j_2,j_2+1}\cdots \overline{j_m,j_m+1}\},\] with its corresponding monomial: \[u'=x_{j_1j_1+1}x_{j_2j_2+1}\cdots x_{j_mj_m+1}.\]
Although the matching \(T_1\) is not symmetric about \(s\), the matching \(T_1\cup T'_1\) is symmetric. The monomial \(uu'\) associated with it forms an eigenvector of \(s\) with eigenvalue \(+1\), as shown previously: \(s(uu')=uu'\).
The number of such eigenvectors equals the number of the matchings \(T_1\cup T_1'\) in \(C_n\) which equals the number of matchings \(T_1\) in \(\{\overline{12}, \overline{23}, \cdots,\overline{\frac{n-1}{2}-1,\frac{n-1}{2}}\}\) which is by (2.17) and (2.21) equal to: \[\label{char2'} [M(\frac{n-1}{2})](q)=F_\frac{n-1}{2}(q)=\sum_{k=0}^{\lfloor\frac{n-1}{4}\rfloor}{\frac{n-1}{2}-k\choose k}q^{k},----(2.37)\] While the number of matchings \(T\cup T'\) equals that of \(T\), but the number of edges in each matching \(T\cup T'\) is \(2k\) compared to \(k\) edges in \(T\). Hence our first contribution to \(\chi(s)\) is \[\label{char3_''} [\chi_1^{}(s)](q)=\sum_{k=0}^{\lfloor\frac{n-1}{4}\rfloor}{\frac{n-1}{2}-k\choose k}q^{2k}=F_{\frac{n-1}{2}}(q^2).----(2.38)\]
We also have another set of matchings symmetric about \(s\). These matchings are formed by adding the edge \(\overline{1n}\) (corresponding variable \(x_{1n}\)), to avoid common vertex with \(\overline{1n}\), but only to each matching: \[T_2\subset\Bigg\{\overline{23},\overline{34}, \cdots,\overline{\frac{n-1}{2}-1,\frac{n-1}{2}}\Bigg\}.\] Let the reflection of \(T_2\) in \(s\) be \(T_2'\), then \(\{\overline{1n}\}\cup T_2\cup T_2'\) is symmetric about \(s\) and its correspondent monomial \(x_{12}ww'\) is an eigenvector of \(s\) with eigenvalue \(-1\), because, as before, we have: \[s(x_{1n}ww')=-x_{12}s(ww')=-x_{12}ww'.\]
The number of such eigenvectors is equal to the number of matchings \(\{\overline{1n}\}\cup T_2\cup T_2'\) in \(C_n\) which is equal to the number of matchings \(T_2\subset\{\overline{23},\overline{34}, \cdots,\overline{\frac{n-1}{2}-1,\frac{n-1}{2}}\}\) which by (2.17) and (2.21) is equal to: \[M(\frac{n-1}{2}-1)=M(\frac{n-3}{2})=F_\frac{n-3}{2}=\sum_{k=0}^{\lfloor\frac{n-3}{4}\rfloor}{\frac{n-3}{2}-k\choose k}q^{k}.\]
However, while the number of matchings \(\{\overline{1n}\}\cup T_2\cup T_2'\) equals that of \(T_2\), but the number of edges in each matching \(\{\overline{1n}\}\cup T_2\cup T_2'\) is \(2k+1\) compared to \(k\) edges in \(T_2\). Hence our 2nd contribution to \(\chi(s)\) is: \[\label{char2''} [\chi_2^{}(s)](q)=-\sum_{k=0}^{\lfloor\frac{n-3}{4}\rfloor}{\frac{n-3}{2}-k\choose k}q^{2k+1}=-qF_{\frac{n-3}{2}}(q^2).----(2.39)\]where the negative sign is due to the \(-1\) eigenvalue above.
Adding Equations (2.38) and (2.39) we arrive at: \[(q)=\sum_{k=0}^{\lfloor\frac{n-1}{4}\rfloor}{\frac{n-1}{2}-k\choose k}q^{2k}-\sum_{k=0}^{\lfloor\frac{n-3}{4}\rfloor}{\frac{n-3}{2}-k\choose k}q^{2k+1},\] with its \(q\)-Fibonacci form according to the total degree decomposition: \[(q)=F_\frac{n-1}{2}(q^2)-qF_\frac{n-3}{2}(q^2).\] This completes the proof. ◻
Example 2.26. For \(n=5\) we have \([\chi(s)](q)=\sum_{k=0}^1{2-k\choose
k}q^{2k}-\sum_{k=0}^0{1-k\choose k}q^{2k+1}={2\choose 0}+{1\choose
1}q^2-{1\choose 0}q=1-q+q^2\).
Let \(q=1\), then \(\chi(s)=1\).
Remark 2.27. For odd \(n\), there is no symmetry in \(C_n\) about \(sr\), therefore we do not discuss the case of \(\chi(sr)\).
Character of \(\overline{FK}_{C_n}(n)\) over \(D_n\) and decomposition
Character of \(\overline{FK}_{C_n}(n)\) over \(D_n\) for even \(n\)
We combine (2.23), (2.26) and (2.34) to obtain the character of \(\overline{FK}_{C_n}(n=\text{even})\) over \(D_n\): \[\label{ceven1}\begin{split} char_{D_n}&[\overline{FK}_{C_n}(n=\text{even})]=\Bigg(\sum_{k=0}^{\frac{n}{2}}\frac{n}{n-k}{n-k\choose k}q^k, 1, 1+gcd(n,p)q^\frac{n}{gcd(n, p)}, 1+\frac{n}{2}q^2,\\&\sum_{k=0}^{\lfloor\frac{n}{4}\rfloor}{\frac{n}{2}-k\choose k}q^{2k}-2\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-1}{2}\rfloor}{\frac{n}{2}-1-k\choose k}q^{2k+1}+\sum_{k=0}^{\lfloor\frac{\frac{n}{2}-2}{2}\rfloor}{\frac{n}{2}-2-k\choose k}q^{2k+2}, \\&\sum_{k=0}^{\lfloor\frac{n-2}{4}\rfloor}{\frac{n-2}{2}-k\choose k}q^{2k}\Bigg)----(3.1). \end{split}\] In terms of \(q\)-Fibonacci/\(q\)-Lucas polynomials, with initial values \(F_0=1\), \(F_1=1\), \(L_0=2\), \(L_1=1\) we obtain: \[\label{ceven1f} \begin{split} char_{D_n}[\overline{FK}_{C_n}(n=\text{even})]=\\\Bigg(L_n(q), ~1, ~\overbrace{1+gcd(n,p)q^{\frac{n}{gcd(n, p)}}}^{(\frac{n}{2}-2)~\text{columns}},~1+\frac{n}{2}q^2,~ F_\frac{n}{2}(q^2)-2qF_{\frac{n}{2}-1}(q^2)+q^2F_{\frac{n}{2}-2}(q^2),~F_\frac{n-2}{2}(q^2)\Bigg), \end{split}\] where \(F_n(q)=\sum_0^{\lfloor\frac{n}{2}\rfloor}{n-k\choose k}q^k\) is the \(q\)-Fibonacci polynomial, and \(1+gcd(n,p)q^{\frac{n}{gcd(n, p)}}\) is a sequence of \((\frac{n}{2}-2)\) terms forming the characters \(\chi(r^p)\) for \(p=2,\cdots, (\frac{n}{2}-1)\).
3.2. Decomposition in irreducible characters
In general a decomposition of a character \(\chi\) in irreducible characters \(\chi^{(i)}\) of a group \(G\), is done according to the following
formula .
\(\chi=\sum_im_i\chi^{(i)},~ \text{with the
coefficients}~
m_i=\langle\chi,\chi^{(i)}\rangle=\frac{1}{|G|}\sum_{K}|K|\chi_K^{}\overline{\chi}_K^{(i)},\)
where the sum is over conjugacy classes.
We write our character in terms of irreducible characters of \(D_n\): \[\label{char5}\begin{split}
char_{D_n}[\overline{FK}_{C_n}(n=\text{even})]=m_{1^n}\chi^{1^n}+m_{2^{\frac{n}{2}}}\chi^{2^{\frac{n}{2}}}&\\+\sum_{2\leq
t\leq
\frac{n}{2}-1,gcd(n,t)\ge
2}m_{(\frac{n}{gcd(n,t)})^{gcd(n,t)}}\chi^{(\frac{n}{gcd(n,t)})^{gcd(n,t)}}+m_{2^{(\frac{n}{2}-1)}11}\chi^{2^{(\frac{n}{2}-1)}11}+m_{2^{\frac{n}{2}'}}\chi^{2^{\frac{n}{2}'}}
\end{split}----(3.3)\] The coefficients of the irreducible
characters are calculated using the character table of \(D_n\), Table 3.2,
with the character \(char_{D_n}[\overline{FK}_{C_n}(n=\text{even})]\)
of Equation 3.2 appearing in the bottom row. We
obtain:
\[\label{coef''}\begin{split} m_{1^n}=\frac{1}{2n}\Bigg\{L_n(q)+2+2\sum_{p=2}^{\frac{n}{2}-1}(1+gcd(n,p)q^\frac{n}{gcd(n, p)})+(1+\frac{n}{2}q^2)\\+\frac{n}{2}\Big[F_{\frac{n}{2}}(q^2)+(1-2q)F_{\frac{n}{2}-1}(q^2)+q^2F_{\frac{n}{2}-2}(q^2)\Big]\Bigg\}\\ m_{n}=\frac{1}{2n}\Bigg\{2L_n+4cos\frac{2\pi}{n}+4\sum_{p=2}^{\frac{n}{2}-1}(1+gcd(n,p)q^\frac{n}{gcd(n,p)})cos\frac{2p\pi}{n}-2(1+\frac{n}{2}q^2)\Bigg\}\\ m_{(\frac{n}{gcd(n,t)})^{gcd(n,t)}}=\frac{1}{2n}\Bigg\{2L_n+4cos\frac{2t\pi}{n}+4\sum_{p=2}^{\frac{n}{2}-1}(1+gcd(n,p)q^\frac{n}{gcd(n,p)})cos\frac{2pt\pi}{n}\\+2(-1)^t(1+\frac{n}{2}q^2)\Bigg\},~2\leq t\leq\frac{n}{2}-1\\ m_{2^{\frac{n}{2}}}=\frac{1}{2n}\Bigg\{L_n(q)+2+2\sum_{p=2}^{\frac{n}{2}-1}(1+gcd(n,p)q^\frac{n}{gcd(n, p)})+(1+\frac{n}{2}q^2)\\-\frac{n}{2}\Big[F_{\frac{n}{2}}(q^2)+(1-2q)F_{\frac{n}{2}-1}(q^2)+q^2F_{\frac{n}{2}-2}(q^2)\Big]\Bigg\}\\ m_{2^{\frac{n}{2}'}}= \frac{1}{2n}\Bigg\{L_n(q)-2+2\sum_{p=2}^{\frac{n}{2}-1}(-1)^p(1+gcd(n,p)q^\frac{n}{gcd(n, p)})+(-1)^{\frac{n}{2}}(1+\frac{n}{2}q^2)\\+\frac{n}{2}\Bigg[F_\frac{n}{2}(q^2)-(1+2q)F_{\frac{n}{2}-1}(q^2)+q^2F_{\frac{n}{2}-2}(q^2)\Bigg]\Bigg\}\\ m_{2^{(\frac{n}{2}-1)}1^2}= \frac{1}{2n}\Bigg\{L_n(q)-2+2\sum_{p=2}^{\frac{n}{2}-1}(-1)^p(1+gcd(n,p)q^\frac{n}{gcd(n, p)})+(-1)^{\frac{n}{2}}(1+\frac{n}{2}q^2)\\-\frac{n}{2}\Bigg[F_{\frac{n}{2}}(q^2)-(1+2q)F_{\frac{n}{2}-1}(q^2)+q^2F_{\frac{n}{2}-2}(q^2)\Bigg]\Bigg\}-----(3.4) \end{split}\]
Example 3.1. Let
\(char_{C_6}[\overline{FK}_{C_6}(6,
q)]=m_{1^6}\chi^{1^6}+m_{2^3}\chi^{2^3}+m_{2^{3'}}\chi^{}_{2^{3'}}+m_{2^21^2}\chi^{2^21^2}+m_{6}\chi^{6}+m_{3^2}\chi^{3^2}\).
Then from Equation 3.4 we have \[m_{1^6}= 1+2q^2,
~m_6=q+q^2,~m_{3^2}=q+2q^2,~m_{2^3}=q+q^3, m_{2^{3'}}=q^2,~m_{2^2
1^2}=q+q^3.\] Substitution of the above coefficients into the
character Equation (3.3) yields: \[\label{char_'}\begin{split}char_{D_6}[\overline{FK}_{C_6}(6,~
q)]=&(1+2q^2)\chi^{1^6}+(q+q^3)\chi^{2^3}+(q^2)\chi^{2^{3'}}\\&+(q+q^3)\chi^{2^21^2}+(q+q^2)\chi^{6}+(q+2q^2)\chi^{3^2}.
\end{split}----(3.5)\]
Sorting in \(q\) we have the decomposition of \(char_{D_6}[\overline{FK}_{C_6}(6)]\) in usual degrees. \[\label{dec_'}\begin{split} char_{D_6}[\overline{FK}_{C_6}(6)]=&\chi^{}_{1^6}+(\chi^{}_{222}+\chi^{}_{2211}+\chi^{}_{6}+\chi^{}_{33})q\\&+(2\chi^{}_{1^6}+\chi^{}_{222'}+\chi^{}_{6}+2\chi^{}_{33})q^2+(\chi^{}_{222}+\chi^{}_{2211})q^3, \end{split}----(3.6)\] which upon putting \(q=1\) reduces to: \[char_{D_6}\overline{FK} _{C_6}(6) =3\chi_{1^6}^{}+2\chi_{222}^{}+\chi_{222'}^{}+2\chi_{2211}^{}+2\chi_{6}^{}+3\chi_{33}^{}.\]
Character of \(\overline{FK}_{C_n}(n)\) over \(D_n\) for odd \(n\) and decomposition
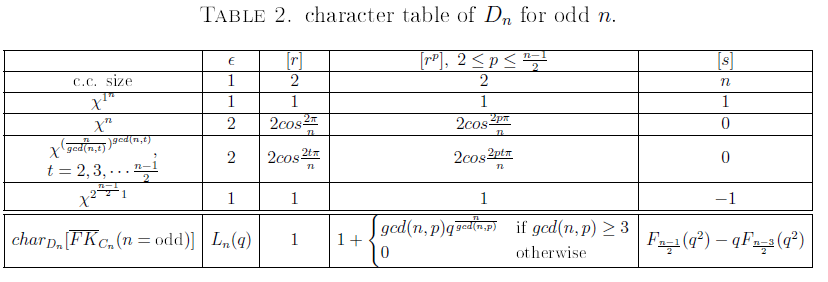
We combine (2.23) and (2.36), to obtain the character of \(\overline{FK}_{C_n}(n=odd)\) over \(D_n\): \[\label{codd}\begin{split} char_{D_n}[\overline{FK}_{C_n}(n=\text{odd})]=&\Bigg( \sum_{k=0}^\frac{n-1}{2}\frac{n}{n-k}{n-k\choose k}q^k,~ 1,~ 1+pq^\frac{n}{p}\delta_{\frac{n}{p},\text{integer}},\\&\sum_{k=0}^{\lfloor\frac{n-1}{4}\rfloor}{\frac{n-1}{2}-k\choose k}q^{2k}-\sum_{k=0}^{\lfloor\frac{n-3}{4}\rfloor}{\frac{n-3}{2}-k\choose k}q^{2k+1}\Bigg)----(3.7). \end{split}\] In terms of \(q\)-Fibonacci/\(q\)-Lucas polynomials, with initial values \(F_0=1\), \(F_1=1\), \(L_0=2\), \(L_1=1\) we have: \[\label{codd'}\begin{split} char_{D_n}[\overline{FK}_{C_n}(n=\text{odd})]=&\Bigg( L_n(q),~1,~\overbrace{1+gcd(n,p)q^{\frac{n}{gcd(n, p)}}}^{(\frac{n-3}{2})~\text{columns}},~F_\frac{n-1}{2}(q^2)-qF_\frac{n-3}{2}(q^2) \Bigg)----(3.8). \end{split}\]
3.4. Decomposition in irreducible characters
Consider the quotient of the Fomin-Kirillov algebra \(\overline{FK}_{C_n}(n=\text{odd})\) associated with the n-cycle subgraph of the complete graph on \(n\) vertices, we have: \[\label{char5'}\begin{split} char_{D_n}[\overline{FK}_{C_n}(n=\text{odd})]=m_{1^n}\chi^{1^n}+ m_{n}\chi^n\\+\sum_{2<t\leq \frac{n-3}{2}}m_{(\frac{n}{gcd(n,t)})^{gcd(n,t)}}\chi^{(\frac{n}{gcd(n,t)})^{gcd(n,t)}}+ m_{(\frac{n}{2})^2}\chi^{(\frac{n}{2})^2}+m_{2^{\frac{n-1}{2}}}\chi_{2^{\frac{n-1}{2}}}. \end{split}----(3.9)\] The coefficients \(m_i\) are calculated using the irreducible characters of \(D_n\) for odd \(n\), as shown in Table 2, where the character of \(\overline{FK}_{C_n}(n)\) appears in the bottom row, and by using formula: \(m_i=\langle\chi,\chi^{(i)}\rangle=\frac{1}{|G|}\sum_{K}|K|\chi_K^{}\overline{\chi}_K^{(i)}\). We obtain the following coefficients.
\[\label{m-odd}\begin{split} m_{1^n}=\\\frac{1}{2n}\Bigg[L_n(q)+2+2\sum_{p=2}^\frac{n-1}{2}\Bigg(1+\begin{cases} gcd(n,p)q^{{\frac{n}{gcd(n, p)}}}&\text{if}~ gcd(n,p)\ge 3\\ 0&\text{otherwise} \end{cases}\Bigg)\\+n\Big(F_{\frac{n-1}{2}}(q^2)-qF_{\frac{n-3}{2}}(q^2)\Big)\Bigg],\\ m_{n}=\\\frac{1}{2n}\Bigg[2L_n(q)+4cos(\frac{2\pi}{n})+4\sum_{p=2}^\frac{n-1}{2}\Bigg(1+\begin{cases} gcd(n,p)q^{{\frac{n}{gcd(n, p)}}}&\text{if}~ gcd(n,p)\ge 3\\ 0&\text{otherwise} \end{cases}\Bigg)cos(\frac{2p\pi}{n})\Bigg],\\ m_{(\frac{n}{gcd(n,t)})^{gcd(n,t)}}=\\\frac{1}{2n}\Bigg[2L_n(q)+4cos(\frac{2t\pi}{n})+4\sum_{p=2}^\frac{n-1}{2}\Bigg(1+\begin{cases} gcd(n,p)q^{{\frac{n}{gcd(n, p)}}}&\text{if}~ gcd(n,p)\ge 3\\ 0&\text{otherwise} \end{cases}\Bigg)cos(\frac{2pt\pi}{n})\Bigg]\\,~2\leq t\leq\frac{n-1}{2},\\ m_{2^\frac{n-1}{2}1}=\\\frac{1}{2n}\Bigg[L_n(q)+2+2\sum_{p=2}^\frac{n-1}{2}\Bigg(1+\begin{cases} gcd(n,p)q^{{\frac{n}{gcd(n, p)}}}&\text{if}~ gcd(n,p)\ge 3\\ 0&\text{otherwise} \end{cases}\Bigg)-n\Big(F_{\frac{n-1}{2}}(q^2)-qF_{\frac{n-3}{2}}(q^2)\Big)\Bigg]----(3.10). \end{split}\]Example 3.2. Let \(n=5\), then \[char_{D_5}[\overline{FK}_{C_5}(5)]=m_{1^5}\chi_{1^5}^{}+ m_{2^21}\chi^{2^21}+m_{5}\chi^5+m_{5'}\chi^{5'},\] where the \(m\)-coefficients derived from Equation (3.10) are: \[m_{1^5}=1+q^2,~ m_{2^21}=q,~m_{5}=q+q^2,~ m_{5'}=q+q^2.\] Substituting these m-coefficients into the character, Equation (3.9), we obtain: \[char_{D_5}[\overline{FK}_{C_5}(5)](q)=(1+q^2)\chi^{1^5}+ q\chi^{2^21}+(q+q^2)\chi^{5}+(q+q^2)\chi^{5'}.\]Sorting the above in terms of \(q\) yields the decomposition in usual degree: \[char_{D_5}[\overline{FK}_{C_5}(5)](q)=\chi^{1^5}+ (\chi^{2^21}+\chi^{5}+\chi^{5'})q+(\chi^{1^5}+\chi^{5}+\chi^{5'})q^2,\] which upon putting \(q=1\) reduces to \[char_{D_5}\overline{FK}_{C_5}(5)=2\chi^{1^5}+\chi^{2^21}+2\chi^{5'}+2\chi^{5}.\]
3.4.1. Representation decomposition of \(D_n\) by conjugation class Since the basis of \(\overline{FK}_{C_n}(n)\) consists of monomials in variables with no common index (alternatively, matchings in an \(n\)-cycle), the \(S_n\)-degree of an element of the basis is product of disjoint \(2\)-cycles and \(1\)-cycles. So it belongs to the \(S_n\)-conjugacy class denoted by \(t_2^kt_1^{n-2k}\) where \(t_2\) and \(t_1\) stand for \(2\)-cycle and \(1\)-cycle respectively and where \(k\) is the degree of monomial. Since we have the same partition of the basis invariant under \(S_n\)-conjugacy class as under usual degree, we have essentially the same decomposition as by usual degree.
3.4.2. Representation decomposition of \(D_n\) by set partition typeSince no two variable appearing in a monomial \(M\in B[\overline{FK}_{C_n}(n)]\) share common indexes, each part of the set partition contains at most \(2\) indexes. Therefore, the set partition type for a degree \(k\) monomial \(M\) is of the form: \[\alpha=(\underbrace{2, 2, \cdots, 2}_k,\underbrace{1, 1, \cdots, 1}_{n-2k}), ~\text{denoted by}~ 2^k1^{n-2k},\] In this notation, each \('2'\) in \(\alpha\) represents an index of a variable if the variable appears in \(M\), while each \('1'\) represents an index that does not appear in any variable in \(M\). Since the partition of the basis remains invariant under set partition type as under usual degree, we essentially have the same decomposition as by usual degree.
Conclusion
We introduced a quotient of the Fomin-Kirillov algebra \(FK(n)\), denoted by \(\overline{FK}_{C_n}(n)\), associated with the \(n\)-cycle subgraph of the complete graph on \(n\) vertices. Through this quotient, We established an interesting connection between the Fomin-Kirillov algebra \(FK(n)\) and the theory of \(q\)-Fibonacci/\(q\)-Lucas polynomials. Specially:
The Hilbert series of this quotient algebra corresponds to the \(q\)-Lucas polynomial.
The dimension of the quotient algebra equals the Lucas number \(L_n\).
We derived general formulas for the character of \(\overline{FK}_{C_n}(n)\) over the Dihedral group \(D_n\) for both even and odd \(n\).
Notably, the representation decomposition of this quotient algebra for usual degree remains essentially the same as for both \(S_n\) degree and set partition degree.
Acknowledgement
I extend my sincere gratitude to Professor Bergeron for reviewing this paper and providing valuable insights.
Conflict of Interests:
The author declares that there is no conflicts of interest.
References
Bärligea, C. (2020). On the dimension of the Fomin-Kirilov Algebra and related algebras, arXiv:2001.04597v1 [math.QA] View
Bazlov, Y. (2006). Nichols-Woronowicz algebra model for Scubert calculus on Coxeter group. J. Algebra 297(2), 372-399, DOI 10.1016/j.jalgebra.2006.01.037. View
Blasiak, J., Liu, R. I., Meszaros, K. (2013). Subalgebras of the Fomin-Kirillov Algebraa, Preprint arXiv:1310.4112 View
Carlitz, L. (1974). "Fibonacci Notes, I. Zero-one Sequences and Fibonacci Numbers of Higher Order," The Fibonacci Quarterly, Vol. 12, No. 1, pp. 1-10.
Cigler, J. Some beautiful q-analogues of Fibonacci and Lucas polynomials, arXiv:1104.2699 [math.HO]. View
Fomin, S. and Kirillov, A. N. (1999). Quadratic algebras, Dunkl elements, and Schubert calculus. Advances in geometry, volume 172 of Progr. Math., pages 147-182. View
Fomin, S. and Procesi, C. (2000). Fibered quadratic Hopf algebras related to Schubert calculus J. Algebra 230(1), 174-183. DOI 10.1006/jabr.1999.7957. View
Anatol, N., Kirillov and Toshiaki, M. (2004). Noncommutative algebras related with Schubert calculus on Coxeter groups. European J. Combin., 25(8):1301-1325. View
Anato,l N. and Kirillov. (2012). On some algebraic and combinatorial properties of Dunkl elements. Internat. J. Modern Phys. B, 26(27-28):1243012, 28. View
Liu, R. I. (2016). On the Commutative Quotient of Fomin-Kirillov Algebra, European Journal of Combinatorics, Volume 54, pages 65-75. View
Mora, T. (1994). An introduction to commutative and noncommutative Grobner bases, Theoretical Computer Science 134, 131-173. View
Sagan, B. E. (2001). The Symmetric Group, Representations, Combinatorial Algorithms, and Symmetric Functions, Second Edition, Springer-Verlag New York, Inc., View
Weisstein, E. W. (2017). The on-line Encyclopedia of Integer Sequences A000032. View