Abstract

Regression analysis is a fundamental statistical technique widely applied in preventive healthcare research to identify risk factors, predict health outcomes, and inform targeted interventions. This in-depth review examines the pivotal role of various regression approaches—linear, logistic, Cox proportional hazards, quantile, linear mixed-effects, multilevel, and Poisson regression—within medical-focused preventive research. The review highlights regression analysis as a powerful tool for analyzing multiple variables simultaneously, quantifying relationships numerically, and minimizing confounding effects to improve the precision of health outcome predictions. It also outlines the advantages of each type of regression and their suitability for different data structures and clinical questions, ranging from simple associations to complex hierarchical and longitudinal analyses. Despite its strengths, regression analysis has limitations, including the need to validate assumptions, issues with multicollinearity and over fitting, challenges with small sample sizes, difficulties in interpreting causality, handling non linear relationships, outliers, missing data, and the complexity of interpreting results. Identifying and managing these challenges is essential for generating valid and actionable findings. In conclusion, the proper use of regression analysis is a critical component of evidence-based preventive strategies, enabling healthcare providers to proactively address health threats and improve both patient and population health outcomes.

Keywords: Prevention, Regression, Medical, Research

Introduction

Clinical practice, epidemiological studies, and the social sciences are key healthcare fields that heavily rely on preventive research methodologies. These investigations—primarily involving primary and secondary prevention—aim to promote health, prevent the onset of diseases and injuries, and detect and halt the progression of asymptomatic or early-stage conditions [1]. Furthermore, they play a critical role in shaping and evaluating health-related policies and regulations, thereby ensuring that public health initiatives are evidence-based and effective. As cornerstones of public health and preventive medicine, such research efforts focus on identifying risk factors, forecasting outcomes, and designing interventions to minimize health threats [2].

However, before drawing valid conclusions or interpreting findings, robust and appropriate statistical analysis is essential. For instance, in a 2019 study by Sung-Woo Kim et al., the researchers aimed to develop a model for estimating health-related physical fitness (HRPF) using easily measurable variables such as gender, age, body mass index, and percent body fat [3]. They employed multiple linear regression techniques to answer critical questions, such as: "Is there a relationship between physical fitness and the future development of chronic disease?" "If so, what is the strength of this relationship?" "Can future outcomes be predicted?" and "Which variables influence this relationship?"

Among the statistical tools used to address such questions, regression analysis stands out for its ability to simultaneously evaluate multiple variables. It allows researchers to interpret data effectively while adjusting for confounders, thereby improving the accuracy of health outcome predictions [2,3]. Regression coefficients offer quantitative insights into how changes in independent variables affect the dependent variable, while the models themselves enable individualized risk prediction and support stratified prevention strategies [3,4].

Despite its utility, the valid application of regression analysis in preventive research requires careful attention to model specification, rigorous data collection, and clear definitions of exposures and outcomes. Researchers must remain mindful of the underlying assumptions for each regression method, as well as potential pitfalls such as multicollinearity, overfitting, and the ecological fallacy, all of which can distort conclusions [4].

This review examines the application of regression analysis in preventive research, emphasizing its importance, mechanisms, and role in informing proactive intervention strategies in general medical practice. It is specifically tailored for early-career clinicians, public health trainees, and graduate students who possess a foundational understanding of biostatistics (e.g., p-values, confidence intervals) and seek structured guidance on how to plan, implement, and interpret regression models in medical contexts.

Regression Analysis: Principles, Types and Advantages

Regression means change in the measurements of a variable, , either positively or negatively, beyond the mean. The imperative principle of regression analysis is its capacity to generate the mathematical relationship that best describes how variables in the study are interrelated. This relationship is typically represented by an equation in which the dependent, (also called outcome, endogenous, explained, response, or predicted variable) variable is expressed as a function of the independent variables (also called exogenous, explanatory, control, or predictor variable), while adjusting for other confounding variables that might affect the exposure- final outcome relationship, and including an error term to account for unexplained variation [2-3].

The equation for multiple regression is typically written as: Y=β0 + β₁X₁+ β₂X₂+ β₃X₃+ ∙ ∙ ∙+βn X n+ϵ. The Y is the dependent variable (outcome), β0 is the intercept (the value of Y when all X variables are zero), β1,β2,β3,…, βn are the coefficients (slopes) for each independent variable (the amount of increase in the dependent variable for an unit increase in the independent variable), X₁,X₂,X₃,…, Xn are the independent variables (predictors), and ϵ is the error term (the amount of variation in Y not explained by the independent variables). When these variables are plotted on a graph, they form a regression line, indicating that the relationship is linear [4,5].

At its core, regression assessment involves a hard and speedy of statistical strategies designed to measure the amount to which changes in the known or predictor variable(s) is /are associated with modifications inside the unknown or response variable. Regression evaluation is a vital device in preventive research as it helps identify and degree the random elements that make a contribution to negative and positive effects and identify the appropriate relationship among variables [3].

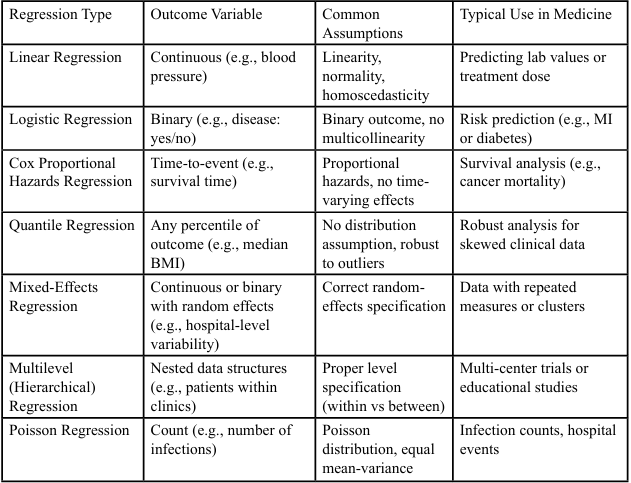
Several types of regression models are commonly employed in preventive research, each tailored to different research questions and data types. Let's discuss a few key regression strategies used in medical research. First, we have linear regression, which is like the reliable classic of statistical techniques. This method assumes a linear relationship between the dependent and independent variables, assuming both variables measured quantitatively [4].

For example, imagine a study investigates how the consumption of fruits and vegetables (predictor) is related to the reduction in systolic blood pressure (response). Linear regression allows to draw a straight line through the data points, showing how these two factors are related. It's quite straightforward when the study considering just one factor, but it becomes more interesting (and complex) when it starts considering multiple factors at once, such as blood cholesterol or body mass index in the above example. Multiple linear regression outspreads this analysis to include multiple confounding variables, facilitating more complex modeling of inhibitory [4,6].

A hypothetical finding for the above investigation is that for every additional serving of fruits and vegetables consumed daily, systolic blood pressure decreases by 1.2 mmHg on average after adjusting of the confounding variables. This analysis facilitated the development of personalized preventive interventions tailored to individual risk profiles, thereby enhancing patient outcomes [3].

The second type, Logistic Regression, which is ideal for binary (dichotomous) outcome variables, assesses the likelihood of an event occurring based on predictor variables. For example, research examining how age, BMI, and family history (independent variables) affect the likelihood of developing type 2 diabetes (dependent variable: yes/no) found that each unit increase in BMI is associated with 1.1 times higher odds of developing type 2 diabetes, controlling for age and family history [7]. Moreover, logistic regression provides insights into the strength and direction of the association between the predictors and the outcome. For instance, in the previous example, it can help identify which factors are most strongly associated with the likelihood of developing type 2 diabetes. This information can be invaluable for developing targeted interventions and preventive measures [8].

The first and second types of logistic regression discussed above are considered standard types, while the third type and beyond are classified as Advanced Regression Techniques. The third type is Cox Proportional Hazards Regression. Although it has a flamboyant name that may scare some physicians, it's extremely beneficial when the study interested in how long it takes for something to happen, such as the progression of a disease. It's a go-to method in survival analysis. For example, a longitudinal study assessing how different treatments (independent variable) affect the time until cancer recurrence (dependent variable) in breast cancer survivors might find that patients receiving Treatment A have a 40% lower risk of cancer recurrence at any given time compared to those receiving the standard treatment, adjusting for age and cancer stage [6,9].

Cox Proportional Hazards Regression is fairly valued in medical studies because of its potential to address censored facts, in which the outcome occasion has now not happened for all topics for the duration of the take a look at length. This technique can accommodate multiple covariates, permitting researchers to manipulate for various confounding elements. Additionally, it gives hazard ratios, which give a clean and interpretable degree of the effect of each predictor on the chance rate. This makes Cox regression a powerful tool for information the elements influencing the timing of events, thereby assisting inside the improvement of powerful remedy strategies and enhancing affected person effects.

The fourth type is Quantile Regression, a powerful statistical method that extends past the limitations of normal least squares regression via analyzing how variables have an effect on different components of the final results distribution. This technique is especially treasured when the connection among variables can also vary throughout exceptional quantiles of the established variable [11]. For example, quantile regression can be used in reading how prenatal pesticide publicity influences exceptional percentiles of cognitive function distribution in youngsters. This type of analysis is essential in environmental epidemiology and developmental psychology, as it can screen nuanced results that might be obscured by way of methods focusing only on the mean. A hypothetical finding might be that better prenatal pesticide publicity is related to extra reductions in cognitive ratings for children inside the decrease quantiles of cognitive feature, suggesting that those with potentially compromised neurodevelopment are extra vulnerable to pesticide outcomes [4]. Such results ought to have tremendous implications for public fitness policies, probably main to more centered interventions for prone populations. Quantile regression consequently offers a greater complete view of the connection among variables, making it an invaluable tool in fields where knowledge the entire spectrum of effects is critical [2,11].

Linear Mixed-Effects Regression, the fifth type, is a powerful statistical technique that extends traditional linear regression by means of incorporating each constant and random outcomes. This approach is especially beneficial for studying hierarchical or clustered facts, consisting of repeated measures or longitudinal research. For instance, it could be hired in investigating how indoor CO2 stages have an effect on cognitive overall performance and productivity in workplace people over time. This sort of analysis is important in occupational health and environmental psychology, as it can account for both populace-level tendencies and character versions [12].

In this situation, constant results would possibly consist of CO2 ranges, time of day, or different managed variables, whilst random consequences ought to account for character differences among people or versions between extraordinary workplace spaces. A hypothetical locating might be that for each 500 ppm increase in indoor CO₂ ranges above a thousand ppm, cognitive take a look at ratings decrease through 15% on average, with big variant among individuals. This result might offer valuable insights into the significance of indoor air nice for cognitive characteristic and productiveness [13].

The sixth kind is Multilevel Regression, additionally referred to as hierarchical linear modeling, that's particularly precious for reading nested records systems where observations are grouped inside better level gadgets. This approach is considerably used in monetary studies and research on profits inequality and health outcomes, allowing researchers to concurrently have a look at effects at multiple ranges of evaluation. For example, multilevel regression can be hired in examining how each man or woman income and societal earnings inequality affect life expectancy. This technique is vital in public health and social epidemiology, as it could disentangle the effects of person-level factors from broader societal impacts [14].

In this situation, the first stage might consist of person traits consisting of personal earnings, schooling, and health behaviors, even as the second one degree may want to encompass county- level factors like earnings inequality (measured by using the Gini coefficient), healthcare machine pleasant, and environmental rules. A hypothetical locating is probably that while person income bills for 25% of the variance in life expectancy, country-stage earnings inequality explains a further 10% of the variance, even after controlling for man or woman factors. This end result could provide compelling proof for the significance of addressing both person and societal factors in improving population fitness effects [6,14].

The last but not least type is Poisson Regression, which is in particular beneficial for modeling matter data and prices of occasions. This technique is especially valuable whilst managing discrete, non-poor outcomes that comply with a Poisson distribution. For instance, Poisson Regression can be used to analyze the connection between network vaccination costs (impartial variable) and the wide variety of influenza cases (based variable) in one of a kind cities over a flu season. This form of analysis is critical in public health and epidemiology for understanding the effectiveness of preventive measures [15].

A hypothetical finding might be that for every 10% boom in vaccination fee, the anticipated number of influenza instances decreases through 15%, protecting populace size steady. This result could offer quantitative evidence for the efficacy of vaccination packages [6].

Poisson Regression gives several blessings over different regression strategies whilst managing rely records. It obviously accounts for the non-bad and discrete nature of the based variable, keeping off the capacity for negative or non-integer predictions that would arise with linear regression. Additionally, it may cope with zero counts efficiently, that's commonplace in lots of real-global eventualities. Poisson Regression additionally permits for the modeling of non linear relationships on a logarithmic scale, making it especially beneficial for records that famous exponential increase or decay. Furthermore, it may contain offset variables to account for one of a kind exposure degrees, allowing truthful comparisons across varying institution sizes or time intervals [2,15].

Table 1: Summary of Key Regression Models in Medical Research

Assumptions, Pitfalls, and Diagnostic Considerations in Regression Analysis

Regression models are powerful tools in preventive research, but their validity hinges on meeting key statistical assumptions and recognizing common pitfalls. One of the most important concerns is multicollinearity, which arises when independent variables are highly correlated, leading to inflated standard errors and unreliable coefficient estimates [3,7]. This issue can be identified using the Variance Inflation Factor (VIF), with values above 10 suggesting problematic collinearity. Overfitting is another critical issue, occurring when a model is overly complex and fits the training data too closely, reducing its generalizability to new data. This can be mitigated by techniques such as cross-validation, LASSO, or Ridge regression. Additionally, linear regression assumes that residuals are normally distributed; this can be assessed using Q-Q plots or the Shapiro-Wilk test, and addressed through variable transformation if necessary [4,6]. Homoscedasticity, or the assumption of constant variance of residuals across levels of the independent variables, can be checked via residual plots and corrected with weighted least squares or transformations. Missing data, if not appropriately handled, can bias results; multiple imputation or maximum likelihood methods are recommended for dealing with non-random missingness [10]. Finally, the presence of outliers and influential observations can significantly distort regression results. Tools such as Cook’s Distance and leverage plots help identify these points, which may require robust regression techniques or sensitivity analysis. Careful attention to these assumptions and pitfalls is essential to ensure that regression analysis provides accurate, interpretable, and actionable findings in preventive medicine [3,7,11].

Challenges and Future Directions

While regression evaluation is a powerful and widely used statistical method, it's miles vital to well-known its barriers and challenges to make sure proper application and interpretation of effects [3,4,6,7,12]:

1. Assumptions: Regression models depend on several key assumptions, which include linearity, independence of mistakes, homoscedasticity, and normality of residuals. Violation of those assumptions can result in biased or unreliable consequences. Researchers have to cautiously test and address any violations, which might also require facts changes or opportunity modeling techniques.

2. Sample size: Small sample sizes may only reveal connections among variables that have a strong relationship. Therefore, the sample size should be determined based on the number of independent variables and the expected strength of the relationships.

3. Multicollinearity: High correlation between independent variables (multicollinearity) can significantly have an effect on model overall performance and interpretation. It can cause unstable estimates of regression coefficients and inflated preferred errors, making it tough to decide the proper effect of man or woman predictors. Techniques like variance inflation component (VIF) evaluation or ridge regression may be essential to deal with this issue.

4. Over-fitting: Building overly complicated fashions with too many predictors relative to the pattern length can bring about over-fitting. These fashions may also perform nicely at the education statistics but fail to generalize to new, unseen records. Cross-validation techniques and regularization methods (e.G., LASSO, Ridge) can assist mitigate overfitting and improve model generalizability.

5. Causality: While regression can become aware of associations between variables, it can't establish causation on its very own. The word "correlation does no longer imply causation" is critical to recollect. Causal inference calls for extra issues, inclusive of take a look at layout, theoretical justification, and often experimental manipulation. Advanced techniques like propensity rating matching or instrumental variable analysis can be needed to method causal questions.

6. Non-linear relationships: Standard regression models count on linear relationships among variables. In truth, many relationships in nature and society are non-linear. Failing to account for non linearity can result in misspecification and terrible version fit. Techniques like polynomial regression, spline features, or non parametric techniques may be important to capture complex relationships appropriately.

7. Outliers and influential points: Regression fashions can be sensitive to outliers and influential factors that can disproportionately have an effect on the outcomes. Careful information examination and strong regression strategies may be required to cope with those problems.

8. Missing statistics: Incomplete datasets are common in actual global studies. How lacking records is handled (e.G., listwise deletion, imputation) can significantly impact regression consequences and have to be carefully considered and pronounced.

9. Interpretation complexity: As fashions end up extra complex, specifically with interaction terms or non-linear components, interpretation can emerge as hard. Clear conversation of results and their sensible importance is crucial.

Identification of such challenges is essential in allowing researchers to apply regression analysis responsibly and effectively. It underscores the importance of rigorous data examination, model specification, and critical interpretation of results. Advanced statistical skills and domain expertise are typically required in overcoming such constraints and extracting meaningful insights from regression analysis [10].

Conclusion

In conclusion, regression models are powerful analytical tools, but they must be applied thoughtfully, with a clear understanding of the types of variables involved and the nature of their relationships. They provide a robust framework for identifying risk factors, predicting outcomes, adjusting for confounding variables, and designing targeted interventions. Their versatility and applicability across various domains—particularly in healthcare—make them essential for proactive approaches to emerging challenges. By harnessing regression analysis effectively, researchers can contribute to the development of evidence-based strategies that prevent adverse outcomes and promote the well-being of individuals and communities.

Conflicts of Interests, and Funding/Supports

There is nothing to be declared

References

1. Murray, D. M. (2017). Prevention research at the National Institutes of Health. Public Health Rep. Sep-Oct;132(5):535-8. View

2. Kim, S. W., Park, H. Y., Jung, H., Lee, J., Lim, K. (2021). Estimation of health-related physical fitness using multiple linear regression in Korean adults: National Fitness Award 2015-2019. Front Physiol. May 13;12:668055. View

3. Ali, P., Younas, A. (2021). Understanding and interpreting regression analysis. Evid Based Nurs. 24:116-8. View

4. Palmer, P. B., & O'Connell, D. G. (2009). Regression analysis for prediction: understanding the process. Cardiopulm Phys Ther J. Sep;20(3):23-6. PMID: 20467520; PMCID: PMC2845248. View

5. Kaya Uyanık, G., Güler, N. (2013). A study on multiple linear regression analysis. Procedia Soc Behav Sci. 106:234-40. View

6. Johnson, A. L., et al. (2018). Multiple linear regression analysis of cardiovascular risk factors. J Prev Cardiol. 12(3):145-59.

7. Joshi, R. D., Dhakal, C. K. (2021). Predicting type 2 diabetes using logistic regression and machine learning approaches. Int J Environ Res Public Health. Jul 9;18(14):7346. View

8. Schober, P., Vetter, T. R. (2021). Logistic regression in medical research. Anesth Analg. Feb 1;132(2):365-6. View

9. David, J., Daniele, G., Van Calster, B., et al. (2023). Ann Intern Med. 176(1):54-61.

10. Faguet, G. B., Davis, H. C. (1984). Regression analysis in medical research. South Med J. 77(6):722-5. View

11. Fasiolo, M., Wood, S. N., Zaffran, M., Nedellec, R., Goude, Y. (2020). Fast calibrated additive quantile regression. J Am Stat Assoc. 116(535):1402-12. View

12. Brown, V. A. (2021). An introduction to linear mixed-effects modeling in R. Adv Methods Pract Psychol Sci. 4(1). View

13. Schneider, A., Hommel, G., Blettner, M. (2010). Linear regression analysis: part 14 of a series on evaluation of scientific publications. Dtsch Arztebl Int. Nov; 107(44):776-82. View

14. Leyland, A. H., Groenewegen, P. P. (2020). Multilevel modelling for public health and health services research: health in context [Internet]. Cham (CH): Springer; 2020. Chapter 3, What is multilevel modelling? 2020 Feb 29. View

15. Roback, D. (2024). Poisson regression. In: Beyond MLR [Internet]. [cited 2024 Oct 29]. html. View