Proof. From the Laplace transform of \(K(x,t)\):
\[\widehat{K}(x,t)=\frac12 s^{-1} \phi^{\frac12}(s) \exp\left\{-\phi^{\frac12}(s)|x| \right\},\] we conclude from the Fourier-Millin formula (e.g., Schiff [22]) for the inversion Laplace transform that \(K(x,t)=\mathcal L^{-1}[\widehat K(s)]\) admits \[K(x,t)=\frac{1}{4\pi i}\int_{\gamma-i\infty}^{\gamma+i\infty} s^{-1}{\phi^{\frac12}(s)}\exp\left\{-\phi^{\frac12}(s)|x| \right\}e^{st}ds,\] where \(\gamma>0\) is any fixed constant, from which we can directly derive the following estimate \[|K(x,t)|\leq\frac{1}{4\pi} \int_{\gamma-i\infty}^{\gamma+i\infty} |s|^{-1} |\phi^{\frac12}(s)| \exp\left\{-\frac{\sqrt{2}}{2}|\phi^{\frac12}(s)||x| \right\}| ds|e^{\gamma t}.\] Moreover, from the definition of \(\phi(s)\), we see that \[|\phi(s)|\geq\sum_{j=1}^\ell q_{j}|s|^{\alpha_{j}}\cos\alpha_{j}\theta \geq\sum_{j=1}^\ell q_{j}|s|^{\alpha_{j}}\cos\alpha_{j}\frac{\pi}{2} \geq c_{0}\sum_{j=1}^\ell |s|^{\alpha_{j}},\] where \(c_{0}:=\min\limits_{1\leq j\leq \ell}\{q_{j}\cos\frac{\alpha_{j}}{2}\pi\}.\) Therefore, \[\begin{aligned} |K(x,t)| &\leq\frac{1}{4\pi} \int_{\gamma-i\infty}^{\gamma+i\infty} |s|^{-1}\left( \sum_{j=1}^\ell q_{j}|s|^{\alpha_{j}} \right)^{\frac12} \exp\left\{-\frac{\sqrt{2}}{2}c_{0}^{\frac12} \left( \sum_{j=1}^\ell |s|^{\alpha_{j}} \right)^{\frac12}|x| \right\}|ds|e^{\gamma t}\\ &\leq\frac{\left(\max\{q_{j}\} \right)^{\frac12}}{4\pi} \int_{\gamma-i\infty}^{\gamma+i\infty} |s|^{-1} \left( \sum_{j=1}^\ell|s|^{\alpha_{j}} \right)^{\frac12} \exp\left\{-\frac{\sqrt{2}}{2}|x|c_{0}^{\frac12} \left( \sum_{j=1}^\ell|s|^{\alpha_{j}} \right)^{\frac12} \right\}|ds|e^{\gamma t}. \end{aligned}\] For short, we denote \(c_1:=\frac{\sqrt{2}}{2}c_{0}^{\frac12}\) and nothing that \(s=\gamma+i\eta\), \(\eta\in(-\infty,+\infty)\), we have \[\begin{aligned} |K(x,t)| &\leq\frac{(\max\{q_{j}\})^{\frac12}}{4\pi} \int_{-\infty}^\infty \frac{\left[\sum_{j=1}^\ell(\gamma^{2}+\eta^{2})^{\frac{\alpha_{j}}{2}} \right]^{\frac12}} {(\gamma^{2}+\eta^{2})^{\frac12}} \exp\left\{-c_1|x| \left[\sum_{j=1}^\ell (\gamma^{2}+\eta^{2})^{\frac{\alpha_{j}}{2}} \right]^{\frac12}\right\} d\eta e^{\gamma t}\\ &=\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_0^\infty \frac{\left[ \sum_{j=1}^\ell(\gamma^{2}+\eta^{2})^{\frac{\alpha_{j}}{2}} \right]^{\frac12}} {(\gamma^{2}+\eta^{2})^{\frac12}} \exp\left\{-c_1|x|\left[ \sum_{j=1}^\ell (\gamma^{2}+\eta^{2})^{\frac{\alpha_{j}}{2}} \right]^{\frac12}\right\} d\eta e^{\gamma t}\\ &=\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_0^\infty \left[\sum_{j=1}^\ell(\gamma^{2}+\eta^{2})^{\frac{\alpha_{j}}{2}-1} \right]^{\frac12} \exp\left\{-c_1|x| \left[ \sum_{j=1}^\ell (\gamma^{2}+\eta^{2})^{\frac{\alpha_{j}}{2}} \right]^{\frac12}\right\} d\eta e^{\gamma t}. \end{aligned}\] By changing the variable \(\eta/\gamma\) to \(\eta\), we find \[\begin{aligned} |K(x,t)| \le\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_0^\infty \left[ \sum_{j=1}^\ell(1+\eta^{2})^{\frac{\alpha_{j}}{2}-1} \gamma^{\alpha_j} \right]^{\frac12} \exp\left\{-c_1|x| \left[ \sum_{j=1}^\ell (1+\eta^{2})^{\frac{\alpha_{j}}{2}} \gamma^{\alpha_j}\right]^{\frac12}\right\} d\eta e^{\gamma t}. \end{aligned}\] We divide the integral on the right-hand side of above inequalities into two parts: \[\begin{aligned} &|K(x,t)| \\ \leq&\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_{0}^{1}\left[\sum_{j=1}^\ell(1+\eta^{2})^{\frac{\alpha_{j}}{2}-1}\gamma^{\alpha_{j}-2}\right]^{\frac12} \exp\left\{-c_1|x| \left[\sum_{j=1}^\ell (1+\eta^{2})^{\frac{\alpha_{j}}{2}}\gamma^{\alpha_{j}} \right]^{\frac12} \right\} d\eta e^{\gamma t}\gamma\\ &+\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_{1}^\infty \left[\sum_{j=1}^\ell(1+\eta^{2})^{\frac{\alpha_{j}}{2}-1}\gamma^{\alpha_{j}-2} \right]^{\frac12} \exp\left\{-c_1|x| \left[ \sum_{j=1}^\ell (1+\eta^{2})^{\frac{\alpha_{j}}{2}}\gamma^{\alpha_{j}} \right]^{\frac12} \right\} d\eta e^{\gamma t}\gamma. \end{aligned}\] We denote the two terms on the right hand side of the above inequality as \(I_1\) and \(I_2\) respectively. We will estimate each of them separately. Firstly, for \(I_1\), we have \[\begin{aligned} I_1(x,t) &\leq \frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_0^1 \left(\sum_{j=1}^\ell\gamma^{\alpha_{j}} \right)^{\frac12} \exp\left\{-c_1|x| \left(\sum_{j=1}^\ell\gamma^{\alpha_{j}} \right)^{\frac12} \right\} d\eta e^{\gamma t}\\ &=\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \left(\sum_{j=1}^\ell\gamma^{\alpha_{j}} \right)^{\frac12} \exp\left\{-c_1|x| \left(\sum_{j=1}^\ell\gamma^{\alpha_{j}} \right)^{\frac12}+\gamma t \right\}. \end{aligned}\] If \(\gamma t\leq1\), a direct calculation implies \[\begin{aligned} I_1(x,t) &\leq \frac{\max\{q_{j}^{\frac12}\}}{2\pi}\left(\sum_{j=1}^\ell \gamma^{\alpha_{j}}\right)^{\frac12}e^{\gamma t} \\ &=\frac{\max\{q_{j}^{\frac12}\}}{2\pi}\sum_{j=1}^\ell(\gamma t)^{\frac{\alpha_{j}}{2}}t^{-\frac{\alpha_{j}}{2}}e^{\gamma t} \leq \frac{e\max\{q_{j}^{\frac12}\}}{2\pi}\sum_{j=1}^\ell t^{-\frac{\alpha_{j}}{2}}, \quad t>0. \end{aligned}\] If \(\gamma t>1\), we take \(\gamma=\gamma_{\ast}\) s.t. \(\gamma_{\ast}t=\frac{c_1}2 |x| \left(\sum_{j=1}^\ell\gamma_{\ast}^{\alpha_{j}} \right)^{\frac12}\) therefore we have \[\begin{aligned} I_1(x,t) &\leq \frac{\max\{q_{j}^{\frac12}\}}{2\pi} \left(\sum_{j=1}^\ell\gamma_{\ast}^{\alpha_{j}} \right)^{\frac12}e^{-\gamma_{\ast}t} =\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \left[ \sum_{j=1}^\ell(\gamma_{\ast}t)^{\alpha_{j}}t^{-\alpha_{j}} \right]^{\frac12} e^{-\gamma_{\ast}t}. \end{aligned}\] Now from the Cauchy-Schwartz inequality, and noting the inequality \[\sum_{j=1}^\ell t^{\alpha_j} e^{-t} \le \sum_{j=1}^\ell (\alpha_j)^{\alpha_j} e^{-\alpha_j} \le \ell,\quad t>0,\] we see that \[\begin{aligned} I_1 (x,t) &\leq \frac{\max\{q_{j}^{\frac12}\}}{2\pi} \left[\sum_{j=1}^\ell \left(\gamma_{\ast}t \right)^{\alpha_{j}} \right]^{\frac12} \left( \sum_{j=1}^\ell t^{-\alpha_{j}} \right)^{\frac12}e^{-\gamma_{\ast}t}\\ &\leq \frac{\ell\max\{q_{j}^{\frac12}\}}{2\pi} \left( \sum_{j=1}^\ell t^{-\alpha_{j}} \right)^{\frac12} \leq \frac{\ell\max\{q_{j}^{\frac12}\}}{2\pi} \sum_{j=1}^\ell t^{-\frac{\alpha_{j}}{2}}, \quad t>0. \end{aligned}\] For \(I_2\), we see that \[\begin{aligned} I_2(x,t) \le \frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_1^\infty \left[\sum_{j=1}^\ell\eta^{\alpha_j-2}\gamma^{\alpha_j-2} \right]^{\frac12} \exp\left\{-c_1|x| \left[\sum_{j=1}^\ell(1+\eta^{\alpha_{j}})\gamma^{\alpha_{j}} \right] ^{\frac12} \right\} d\eta e^{\gamma t}\gamma. \end{aligned}\] Moreover, by a direct calculation, it is not difficult to see that \[\left(\sum_{j=1}^\ell a_j \right)^{\frac12} \le \sum_{j=1}^\ell a_j^{\frac12},\quad \mbox{for $a_j\ge0$,}\] and then \[\begin{aligned} &I_2(x,t) \\ \leq& \frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_1^\infty \left( \sum_{j=1}^\ell\eta^{\frac{\alpha_{j}}{2}-1}\gamma^{\frac{\alpha_{j}}{2}} \right) \exp\left\{-c_1|x|\sum_{j=1}^\ell(1+\eta^{\frac{\alpha_{j}}{2}}) \gamma^{\frac{\alpha_{j}}{2}} \right\} d\eta e^{\gamma t}\\ =&\frac{\max\{q_{j}^{\frac12}\}}{2\pi} \int_1^\infty \left( \sum_{j=1}^\ell\eta^{\frac{\alpha_{j}}{2}-1}\gamma^{\frac{\alpha_{j}}{2}} \right) \exp\left\{-c_1|x|\sum_{j=1}^\ell\eta^{\frac{\alpha_{j}}{2}} \gamma^{\frac{\alpha_{j}}{2}} \right\} d\eta \exp\left\{\gamma t-c_1|x|\sum_{j=1}^\ell\gamma^{\frac{\alpha_{j}}{2}} \right\} \\ \leq& \frac{\max\{q_{j}^{\frac12}\}}{\pi\min\{\alpha_j\}} \int_1^\infty \exp\left\{-c_1|x|\sum_{j=1}^\ell \eta^{\frac{\alpha_{j}}{2}}\gamma^{\frac{\alpha_{j}}{2}} \right\} d\left(\sum_{j=1}^\ell\eta^{\frac{\alpha_j}{2}}\gamma^{\frac{\alpha_{j}}{2}} \right) \exp\left\{\gamma t-c_1|x|\sum_{j=1}^\ell\gamma^{\frac{\alpha_{j}}{2}} \right\}\\ \leq& \frac{\max\{q_{j}^{\frac12}\}}{\pi\min\{\alpha_j\}} \frac{\exp\left\{-c_1|x|\sum_{j=1}^\ell\gamma^{\frac{\alpha_{j}}{2}} \right\}} {c_1|x|} \exp\left\{\gamma t-c_1|x|\sum_{j=1}^\ell\gamma^{\frac{\alpha_{j}}{2}} \right\}\\ =&\frac{\sqrt{2}\max\{q_{j}^{\frac12}\}}{\pi\sqrt{c_0}\min\{\alpha_j\}} \frac1{|x|} \exp\left\{\gamma t-c_1|x|\sum_{j=1}^\ell\gamma^{\frac{\alpha_{j}}{2}} \right\}. \end{aligned}\] If \(\gamma t > 1\), we take \(\gamma=\gamma_{\ast}\) s.t. \(\gamma_{\ast}t=\frac{c_{1}}{2}|x|\sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}}\), therefore \[\begin{aligned} I_2(x,t) &\leq \frac{\sqrt{2}\max\{q_{j}^{\frac12}\}}{\pi\sqrt{c_0}\min\{\alpha_j\}} \frac1{|x|}e^{-\gamma_{\ast}t} \leq \frac{\max\{q_{j}^{\frac12}\}}{2\pi\min\{\alpha_j\}}\frac{1}{t}\sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}-1}e^{-\gamma_{\ast}t}\\ &=\frac{\max\{q_{j}^{\frac12}\}}{2\pi\min\{\alpha_j\}}t^{-1}\sum_{j=1}^\ell(\gamma_{\ast}t)^{\frac{\alpha_{j}}{2}-1}t^{1-\frac{\alpha_{j}}{2}} e^{-\gamma_{\ast}t} \leq C\sum_{j=1}^\ell t^{-\frac{\alpha_{j}}{2}}, \quad t>0. \end{aligned}\] If \(\gamma t\leq1\), we take \(\gamma=\gamma_{\ast}\) s.t. \(\gamma_{\ast}t=2c_{1}|x|\sum_{j=1}^\ell\gamma^{\frac{\alpha_{j}}{2}}\), therefore \[\begin{aligned} I_2(x,t) &\leq\frac{C}{|x|} \exp\left\{-c_{1}|x|\sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}} \right\}\\ &=\frac{C}{|x|\sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}}} \exp\left\{-c_{1}|x|\sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}} \right\} \sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}}\\ &\leq C\sum_{j=1}^\ell\gamma_{\ast}^{\frac{\alpha_{j}}{2}} =C\sum_{j=1}^\ell(\gamma_{\ast}t)^{\frac{\alpha_{j}}{2}}t^{-\frac{\alpha_{j}}{2}} \leq C\sum_{j=1}^\ell t^{-\frac{\alpha_{j}}{2}},\quad t>0, \end{aligned}\] which finishes the proof of the first part of the lemma.

For evaluating \(D_t^{1-\alpha}K\) with \(\alpha>\frac{\alpha_1}2\), we first calculate its Laplace tranform \(\mathcal L[D_t^{1-\alpha}K]\). Indeed, in view of the formula \[\mathcal L\{D_t^\alpha f(t);s\} = s^\alpha \mathcal L\{f(t);s\} - J^{1-\alpha} f(0+).\] Moreover, since \(|K(x,t)|\le C\sum_{j=1}^\ell t^{-\frac{\alpha_j}2}\), we have \(J^\alpha K(x,t)\) tends to \(0\) as \(t\to0\), hence a direct calculation yields \[\mathcal L\{ D_t^{1-\alpha} K(x,t);s\} = s^\alpha \widehat K(s).\] Now following the above argument for (2.2), the desired result in (2.3) can be proved. ◻

Remark 2.1.

This result parallelly generalized the estimates of the fundamental solution in Kochubei [8, Proposition 1] to the multi-term time-fractional case. However, based on our calculation, we must assume a condition \(2\alpha_\ell>\alpha_1\). The estimate for the fundamental solution without this assumption remains open.

Fractional Theta function

A representation of the solution to the initial-boundary value problem in a bounded domain can be constructed via the usual Theta function for the heat equation Cannon [2]. We consider the generalization of this function by \[\theta (x,t) = \sum_{m=-\infty}^\infty K(x+2m,t),\quad t>0.\] Now investigate the Laplace transform of the fractional Theta function \(\theta\) with respect to time variable \(t\in(0,\infty)\). Indeed, from the definition of \(\theta\) and the Laplace transform of the fundamental solution to (2.1), we see that \[2\mathcal L \{\theta(x,t);s\}=s^{-1}\phi^{\frac12}(s) \sum_{m=-\infty}^\infty e^{-|x+2m|\phi^{\frac12}(s)}.\] For \(x\in[0,1]\), we further have \[\begin{aligned} 2\mathcal L \{\theta(x,t);s\} &=s^{-1}\phi^{\frac12}(s) \left( e^{x\phi^{\frac12}(s)} \sum_{m=-\infty}^{-1}e^{2m\phi^{\frac12}(s)} +e^{-x\phi^{\frac12}(s)} \sum_{m=0}^\infty e^{-2m\phi^{\frac12}(s)} \right) \\ &=\frac{\phi^{\frac12}(s)}{s} \left( e^{x\phi^{\frac12}(s)} \sum_{m=1}^\infty e^{-2m\phi^{\frac12}(s)}+ e^{-x\phi^{\frac12}(s)}\sum_{m=0}^\infty e^{-2m\phi^{\frac12}(s)} \right) \\ &=\frac{\phi^{\frac12}(s)}{s} \frac{e^{x\phi^{\frac12}(s)}}{e^{2\phi^{\frac12}(s)}-1} +\frac{\phi^{\frac12}(s)}{s} \frac{e^{(2-x)\phi^{\frac12}(s)}}{e^{2\phi^{\frac12}(s)}-1},\quad s>0. \end{aligned}\] From the definition of the fractional Theta function, it is not difficult to see that \(\theta(1,0)=0\), we are led to \[\begin{aligned} \mathcal L\{ \theta (1,t);s \} =\frac{\phi^{\frac12}(s)}{s}\frac{e^{\phi^{\frac12}(s)}}{e^{2\phi^{\frac12}(s)}-1}, \quad s>0. \end{aligned}\]

As an application of the fractional Theta function \(\theta(x,t)\), we can obtain a representation formula of the solution to (3.2) can by obtained.

Lemma 2.3

For piecewise-continuous functions \(u_0\), \(g_0\) and \(g_1\), the solution of \[\label{eq-IBVP} \left\{ \begin{alignedat}{2} &\sum_{j=1}^\ell q_j\partial_t^{\alpha_j} u-\partial_x^2 u = 0 &\quad& \mbox{in }(0,1)\times(0,T), \\ &u(\cdot,0)=u_0 &\quad& \mbox{in } (0,1), \\ &u_x(0,\cdot)=g_0,\ u_x(1,\cdot)=g_1 &\quad& \mbox{in } (0,T)-----------(2.4) \end{alignedat} \right.\] has the form \[u=w(x,t)+v_1(x,t)+v_2(x,t),\quad (x,t)\in(0,1)\times(0,T),\] where \[w(x,t)=\int_0^1 (\theta (x-\xi,t)+\theta (x+\xi,t))u_0 (\xi) d\xi,\] \[v_1(x,t) = 2\int_0^t \theta(x,t-\tau) G_0(\tau)d\tau,\] and \[v_2(x,t) = 2\int_0^t \theta(x-1,t-\tau) G_1(\tau)d\tau\] with \(G_0,G_1\) satisfying \[\begin{aligned} g_0(t) &= \sum_{j=0}^\ell q_j J^{1-\alpha_j} G_0 \\ g_1(t) &= \sum_{j=0}^\ell q_j J^{1-\alpha_j} G_1. \end{aligned}\]

The proof is extremly similar to the argument used in Rundell, Xu and Zuo , so we omit the proof of this lemma.

Proof of the main result

Cauchy problem

Now let us turn to considering the following lateral Cauchy problem \[\label{eq-cauchy} \left\{ \begin{alignedat}{2} &\sum_{j=1}^\ell q_j \partial_t ^{\alpha_j }u=\partial_x^2 u &\quad& \mbox{in }(0,1)\times(0,T), \\ &u(0,\cdot)=u_x(0,\cdot)=0 &\quad& \mbox{in }(0,T).-------------(3.1) \end{alignedat} \right.\] We first set \(u_0 (x):=u(x,0)\) and \(g(t)=u_x(1,t)\), we extend the function \(g\) to the interval \([0,+\infty)\) by letting \(g\equiv0\) outside of \((0,T)\), and by \(\widetilde{g}\) we denote the extension, and by \(\widetilde{u}\) we denote the solution to the following auxiliary sysytem \[\label{eq-free_t} \left\{ \begin{alignedat}{2} &\sum_{j=1}^\ell q_j\partial_t^{\alpha_j}\widetilde{u}-\partial_x^2\widetilde{u}=0 &\quad& \mbox{in }(0,1)\times(0,+\infty), \\ &\widetilde{u}(\cdot,0)=u_0 &\quad& \mbox{in } (0,1), \\ &\widetilde{u}_x(0,\cdot)=0,\ \widetilde{u}_x(1,\cdot)=\widetilde{g} &\quad& \mbox{in } (0,+\infty).---------------(3.2) \end{alignedat} \right.\]

Remark 3.1.

From the estimates for the fundamental solution in Lemma 2.2, following the argument used in Li and Yamamoto [10, Lemma 2.2], one can easily show that there exist positive constants \(C\) and \(M\) such that \[\label{esti-u(0,t)} |\widetilde u(0,t)| \le Ce^{Mt},\quad t>0.\]-------------(3.3)

We will prove that the boundary \(\widetilde u(0,\cdot)=0\) in \((0,T)\) combined with (3.2) can uniquely determine the initial and boundary value, that is, \(u_0=0\) and \(\widetilde g=0\), which further implies the uniqueness of the lateral Cauchy problem (3.1).

Lemma 3.1.

Let \(T>0\) be a fixed constant and \(u\in L^2 (0,T;H^{2}(0,1))\) be a solution to the lateral Cauchy problem (3.1). Then we have \[u(x,t)=0, \quad (x,t)\in [0,1]\times[0,T].\]

Proof.

Proof. From the above calculations and settings, and noting lemma, we see that \(\widetilde{u}\) is an extension of \(u\) which solves the Cauchy problem (3.1), that is \(\widetilde{u}=u\) in \([0,1]\times[0,T]\). Using the assumption that \(u(0,t)=0\) for \(t\in[0,T]\), we find \[2\int_0^1 \theta (\xi,t)u_0 (\xi) d\xi +2\int_0^t \theta(1,t-\tau) \widetilde G(\tau) d\tau =\begin{cases} 0, &t\in(0,T),\\ \widetilde{u}(0,t), & t\in[T,+\infty). \end{cases}\] Here \(G\) is such that \[\widetilde g(t) = \sum_{j=1}^\ell q_j J^{1-\alpha_j} \widetilde{G}(t).\] It is not difficult to check that the Laplace transform for \(\widetilde G\) can be calculated by \[\mathcal L\{\widetilde G;s\} = \frac{s\mathcal L \{\widetilde g;s\} } { \phi(s)}, \quad \phi(s):=\sum_{j=1}^\ell q_j s^{\alpha_j}.\] Taking the Laplace transforms on both sides of the above equation, we have \[\label{eq-lap-u} 2\int_0^1 \mathcal L\{\theta (\xi,t);s\}u_0 (\xi) d\xi +2\mathcal L\{\theta (1,t);s\} \frac{s\mathcal L \{\widetilde g;s\} }{ \phi(s) } =\int_T^\infty \widetilde{u}(0,t)e^{-st} dt ,\] where \(\mathcal L \{\varphi;s\}\) means the Laplace transform of a function \(\varphi\).

Combining the above calculation, form (3.4), we find that

From the choice of \(\widetilde{g}\), we see that \[\mathcal L\{\widetilde{g}(t);s\} =\int_0^T g(t)e^{-st} dt \leq\|g\|_{L^\infty (0,T)}\int_0^T e^{-st} dt \leq\|g\|_{L^\infty (0,T)}s^{-1}, \quad s>0.\]

Moreover, from the estimate (3.3), it follows that \[\int_T^\infty |\widetilde{u}(0,t)|e^{-st} dt \leq \int_T^M Ce^{(M-s)t} dt =\frac{Ce^{MT}}{s-M}e^{-sT},\quad s>2M.\]

Then for \(I_1\), we have \[\begin{aligned} |I_{1}(s)| &\leq \frac12 \phi^{\frac12}(s) \left( e^{\phi^{\frac12}(s)}-e^{-\phi^{\frac12}(s)} \right) \frac{Ce^{MT}}{s-M}e^{-sT} \\ &=\frac12 \left( e^{(\sum_{j=1}^\ell q_j s^{\alpha_j })^{\frac12}}-e^{-(\sum_{j=1}^\ell q_j s^{\alpha_j })^{\frac12}} \right) \frac{Ce^{MT}}{s-M}e^{-sT} \\ &\leq Ce^{-C_{1}s}, \quad s>2M. \end{aligned}\] For \(I_{2}\), since \(u_0 :=u(\cdot,0)\in C[0,1]\), we have \[\begin{aligned} |I_{2}(s)| &\leq\frac{\phi(s)}{s} \|u_0 \|_{L^\infty (0,1)} \int_0^1 e^{(\xi-1)\phi^{\frac12}(s)} d\xi \\ &\leq C \|u_0 \|_{L^\infty (0,1)} (1-e^{-\phi^{\frac12}(s)}) \leq C\|u_0 \|_{L^\infty (0,1)} s^{\alpha_\ell - 1}, \quad s>1. \end{aligned}\] We then have \[|I_{3}(s)|\leq ce^{-c_{1}s}+\|g\|_{L^\infty (0,T)}s^{-1} +\frac12\|u_0 \|_{L^\infty (0,1)}s^{\alpha_\ell-1}, \quad s>2M,\] which further implies \[\left|\int_0^1 e^{(1-\xi)\phi^{\frac12}(s)}u_0 (\xi) d\xi \right| \leq c_{2}(1+s^{\alpha_\ell}), \quad s>2M.\] The change of variables implies \[\left|\int_0^1 e^{\eta z}u_0 (1-\eta){d\eta}\right| \leq c_{2}z^{\gamma}, \quad \gamma\mbox{ large enough}, \ z>2M.\] For \(0<|z|<2M\), we have \[\left|\int_0^1 e^{\eta z}u_0 (1-\eta){d\eta} \right| \leq\|u_0 \|_{L^\infty (0,1)}e^{z} \leq\|u_0 \|_{L^\infty (0,1)}e^{2M}.\] Therefore \[\left|\int_0^1 e^{\eta z}u_0 (1-\eta){d\eta}\right| \leq c_{3}e^{az}, \quad z>0.\]

From Phragmèn-Lindelöf principle, following the argument used in [10, Corollary 2.1], we must have \[u_0 \equiv0\quad \mbox{ in }[0,1].\] We next use Titchmarsh convolution theorem (see Doss [4] and Titchmarsh [21]) to derive that \(\widetilde{g}(t)\equiv0\), \(t>0\), then \(g\equiv0\). From the uniqueness of the initial-boundary value problem (3.2), we see that \(\widetilde{u}\equiv0\), that is \(u\equiv0\), we finish the proof of the lemma. ◻

Proof of the main result

Theorem-1 directly follows from the above lemmas.

Proof.

Proof of Theorem 1. Indeed, setting \(I=(a,b)\) with \((a,b)\subset[0,1]\), by \(u|_{I\times(0,T)}\), we have \(u(a,\cdot)=u_x(a,\cdot)=0\) and \(u(b,\cdot)=u_x(b,\cdot)=0\) in \((0,T)\), changing independent variables \(x\rightarrow a-x\) and \(x\rightarrow x-b\) in the intervals \((0,a)\) and \((b,1)\) respectively, and applying lemma (3.1), we obtain \(u\equiv0\) in \((0,a)\times(0,T)\) and \((b,1)\times(0,T)\). ◻

Numerical simulation

On account of the theoretical uniqueness result explained in the previous section, this section is primarily intended to develop an effective numerical method. that is, the numerical reconstruction of the solution in the domain \((0,1)\times (0,T)\) from the addition data \(u\) in \(I\times(0,T)\), where \(I\) is a subinterval of \((0,1)\).

Iterative thresholding algorithm

We consider the initial-boundary value problem for a single-term time-fractional diffusion equation with homogeneous Dirichlet boundary condition \[\label{eq-a=0} \left\{ \begin{alignedat}{2} &\partial_t^\alpha u - \Delta u = 0, &\quad& (x,t) \in (0,1)\times(0,T), \\ &u(x,0)=a(x), &\quad& x\in (0,1), \\ &u(0,t)=u(1,t)=0, &\quad& t\in (0,T).---------------(4.1) \end{alignedat} \right.\] In order to emphasize that the solution of problem (4.1) depends on the unknown function \(a\), we write it as \(u(a)\).

Lemma 4.1.

[5, Lemma 3.4] For \(\alpha>0\) and \(g_{1},g_{2}\in L^{2}(0,T)\), there holds \[\int_{0}^{T}(J_{0+}^{\alpha}g_{1}(t))g_{2}(t)dt= \int_{0}^{T}g_{1}(t)J_{T-}^{\alpha}g_{2}(t)dt,\] where \(J_{T-}^\alpha g\) denotes the \(\alpha\)-th order backward integrals of \(g\) are defined by \[J_{T-}^\alpha g(t) = \frac1{\Gamma(\alpha)} \int_t^T (\tau-t)^{\alpha-1} g(\tau) d\tau,\quad t\in(0,T).\]

From this, we set \(a_{true}\in L^{2}(0,1)\) as the true solution to problem (4.1), and by using noise contaminated observation data \(u^{\delta}\) in \(I\times(0,T)\), we carry out numerical reconstruction. Where \(u^{\delta}\) satisfies \(\|u^{\delta}-u(a_{true})\|_{L^{2}(I\times(0,T))}\leq\delta\) and \(\delta\) stands for the noise level. For avoiding ambiguity, we specify \(u^{\delta}=0\) out of \(I\times(0,T)\) so that it is well-defined in \((0,1)\times(0,T)\).
By using the Tikhonov regularization technique, we can transform the reconstruction of the initial value into the minimization of the following output least squares functional \[\label{min} \min\limits_{a\in L^{2}(0,1)} \Phi(a),\quad \Phi(a):=\|u(a)-u^{\delta}\|_{L^{2}(I\times(0,T))}^{2} +\rho\|a\|_{L^{2}(0,1)}^{2},\]---------(4.2) where \(\rho>0\) is the regularization parameter.
Now we need the information about the Fréchet derivative \(\Phi'(a)\) of the objective functional \(\Phi(a)\). For an arbitrarily fixed direction \(g\in L^{2}(0,1)\), it follows from direct calculations that \[\begin{aligned} \label{fre} \Phi'(a)g &=2\int_{0}^{T}\int_{I}(u(a)-u^{\delta})(u'(a)g)dxdt +2\rho\int_{0}^{1}agdx \nonumber\\ &=2\int_{0}^{T}\int_{I}(u(a)-u^{\delta})u(g)dxdt +2\rho\int_{0}^{1}agdx.--------------(4.3) \end{aligned}\] Here \(u'(a)g\) denotes the Fréchet derivative of \(u(a)\) in the direction \(g\), and the linearity of (4.1) immediately yields \[u'(a)g=lim_{\epsilon\rightarrow0}\frac{u(a+\epsilon g)-u(a)}{\epsilon}=u(g).\] It is clear that using (4.3) to evaluate \(\Phi'(a)g\) for all \(g\in L^{2}(0,1)\) is extremely expensive, since one should solve system (4.1) for \(u(g)\) with \(g\) varying in \(L^{2}(0,1)\) in the computation for a fixed \(a\). We introduce the adjoint system of (4.1) to reduce the computational costs for the Fréchet derivatives, that is, the following system for a backward time-fractional diffusion equation \[\label{eq-back} \left\{ \begin{alignedat}{2} &D_{T}^{\alpha}v+\Delta v=\chi_{I}(u(a)-u^{\delta}),&\quad& (x,t) \in (0,1)\times(0,T), \\ &J_{T}^{1-\alpha}v(x,T)=0, &\quad& x\in (0,1),\\ &v(0,t)=0,v(1,t)=0, &\quad& t\in (0,T),-----------(4.4) \end{alignedat} \right.\] where \(D_{T}^{\alpha}u\) stands for the backward Riemann-Liouville derivative of \(u\) which is defined by \(D_T^\alpha u:= \partial_t J_{T-}^{1-\alpha}u\), and \(\chi_{I}\) denotes the characterization function of \(I\), and we write the solution of (4.4) as \(v(a)\).
We can further treat the first term in (4.3) as \[\begin{aligned} \int_{0}^{T}\int_{I}(u(a)-u^{\delta})u(g)dxdt =&\int_{0}^{T}\int_{0}^{1}\chi_{I}(u(a)-u^{\delta})u(g)dxdt\\ =&\int_{0}^{T}\int_{0}^{1}(D_{T}^{\alpha}v+\Delta v)u(g)dxdt\\ =&-\int_{0}^{1}J_{T}^{1-\alpha}v_{a}(0)gdx, \end{aligned}\] implying \[\Phi'(a)g=2\int_{0}^{1}(\rho ag-J_{T}^{1-\alpha}v_{a}(0)g)dx, \quad \forall g\in L^{2}(0,1).\] This suggests a characterization of the solution to the minimization problem (4.2).

Lemma 4.2.

The function \(a^{\ast}\in L^{2}(0,1)\) is a minimizer of the functional \(\Phi(a)\) in (4.2) only if it satisfies the variational equation \[\label{eq=0} \rho a^{\ast}g-J_{T}^{1-\alpha}v_{a^{\ast}}(0)g=0,\]----------(4.5) where \(v_{a^{\ast}}(0)\) solves the backward problem (4.4) with the coefficient \(a^{\ast}\).

We can obtain the iterative thresholding algorithm by adding \(Ma^{\ast}(M>0)\) to both sides of (4.5) and rearranging the equation, \[\begin{aligned} \label{eq-itera} a_{k+1} =&\frac{M}{M+\rho}a_{k}+\frac{1}{M+\rho}J_{T}^{1-\alpha} v_{a_{k}}(0)\nonumber\\ =&\frac{M}{M+\rho}a_{k}+\frac{1}{M+\rho}\frac{1}{\Gamma(1-\alpha)} \int_{t}^{T}(\tau-t)^{-\alpha}v_{a_{k}}(x,\tau)d\tau|_{t=0}\nonumber\\ =&\frac{M}{M+\rho}a_{k}+\frac{1}{M+\rho}\frac{1}{\Gamma(1-\alpha)} \int_{0}^{T}\tau^{-\alpha}v_{a_{k}}(x,\tau)d\tau,-------------(4.6) \end{aligned}\] Where \(M>0\) is a tuning parameter for the convergence, it suffices to choose
\[M\geq\|A\|^{2}_{op},\quad where\] \[\begin{aligned} \label{eq-M} A:L^{2}(0,1)&\rightarrow L^{2}(I\times(0,T)),\nonumber\\ a&\mapsto u(a)|_{I\times(0,T)}.--------------(4.7) \end{aligned}\] Here \(\|\cdot\|_{op}\) denotes the operator norm of an operator under consideration. There is the iterative thresholding algorithm for the reconstruction of the initial value.

Algorithm 4.1.

Choose a tolerance \(\varepsilon>0\), a regularization parameter \(\rho>0\) and a tuning constant \(M>0\) according to (4.7). Give an initial guess \(a_{0}\in L^{2}(0,1)\), and set \(k=0\).
1.Compute \(a_{k+1}\) by the iterative update (4.6).
2.If \(\|a_{k+1}-a_{k}\|_{L^{2}(0,1)}/\|a_{k}\|_{L^{2}(0,1)}<\varepsilon\), stop the iteration. Otherwise, update \(k\leftarrow k+1\) and return to Step 1.

As can be seen from (4.6), we only need to solve the forward problem (4.1) once for \(u(a_{k})\) and the backward problem (4.4) once for \(v(a_{k})\) subsequently at each iteration step. Therefore, the numerical implementation of Algorithm 1 is easy and computationally cheap.

As a result, for the adjoint system of (4.4), we know that \(v(a)\) is the solution to the following problem with the Caputo derivative \[\label{eq-caputo} \left\{ \begin{alignedat}{2} &-\partial_{t}^{\alpha}(v)+\Delta v=\chi_{I}(u(a)-u^{\delta})&\quad& \mbox{in } (0,1)\times(0,T),\\ &v=0 &\quad& \mbox{in } (0,1)\times\{0\},\\ &v(0,t)=v(1,t)=0 &\quad& \mbox{in } (0,T),------------(4.8) \end{alignedat} \right.\] because of the homogeneous terminal value \(J_{T-}^{1-\alpha}v(\cdot,T)=0\), it suffices to deal with (4.8) instead of (4.4) by the same forward solver for (4.1) in the numerical simulation.

Numerical experiments

In this section, we will apply the iterative thresholding algorithm established in the previous subsection to the numerical treatment of unique continuation of the solution, that is, the identification of the value of the solution in \((0,1)\times(0,T)\) from the addition data \(u|_{I\times(0,T)}\). We will illustrate the effectiveness of the reconstruction method through a large number of test examples.

With the true solution \(a_{true}\in L^{2}(0,1)\),we produce the noisy observation data \(u^{\delta}\) by adding uniform random noises to the true data,i.e \[u^{\delta}(x,t)=(1+\delta rand(-1,1))u(a_{true})(x,t), \quad (x,t)\in I\times(0,T).\] Here rand(-1,1) denotes the uniformly distributed random number in [-1,1] and \(\delta\geq0\) is the noise level.
In addition to illustrative graphs, we mainly use the relative \(L^{2}\)-norm error to evaluate numerical performance \[err_{a}:=\frac{\|a_{r}-a_{true}\|_{L^{2}(0,1)}}{\|a_{true}\|_{L^{2}(0,1)}}\] where \(a_{r}\) is regarded as the reconstructed solution produced by Algorithm (4.1).

Then, we study the solution of the direct problem, the numerical solution obtained by difference scheme is compared with the reconstructed solution obtained by inversion algorithm, we evaluate the numerical performance by the relative \(L^{2}\)-norm error \[err_{u}:=\frac{\|u_{r}-u_{n}\|_{L^{2}(0,1)}}{\|u_{n}\|_{L^{2}(0,1)}}\] Where \(u_{r}\) stands for the reconstructed solution and \(u_{n}\) denotes the numerical solution.

We divide the space-time region \([0,1]\times[0,1]\) into \(40\times40\) equidistant meshes. First we fix the noise level \(\delta=0.5\%\) and the observation subdomain \(I=(0,0.05)\cup(0.95,1)\) and test the algorithm with the following settings:
\((a)\quad \alpha=0.2,\quad M=8\times10^{-4},\quad \rho=10^{-7}\), \(a_{true}(x)=\frac{sin(\pi x)-x(x-1)}{\Gamma(2-\alpha)}\),
initial guess \(a_{0}(x)=13\),set the tolerance parameter \(\varepsilon=10^{-4}\).
\((b)\quad \alpha=0.4,\quad M=9\times10^{-4},\quad \rho=9\times10^{-9}\), \(a_{true}(x)=\frac{x-x^{2}}{\Gamma(2-\alpha)}\),
initial guess \(a_{0}(x)=3\),set the tolerance parameter \(\varepsilon=10^{-4}\).
\((c)\quad \alpha=0.3,\quad M=10^{-4},\quad \rho=10^{-7}\), \(a_{true}(x)=(x-1)(e^{x}-1)\),
initial guess \(a_{0}(x)=-8\),set the tolerance parameter \(\varepsilon=4\times10^{-4}\).
\((d)\quad \alpha=0.3,\quad M=10^{-4},\quad \rho=10^{-7}\), \(a_{true}(x)=1-|2x-1|\),
initial guess \(a_{0}(x)=-8\),set the tolerance parameter \(\varepsilon=4\times10^{-4}\).

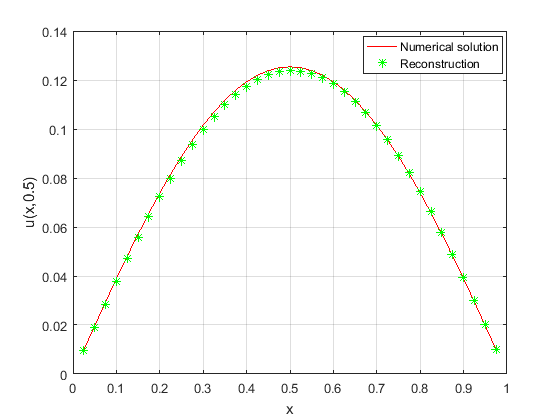
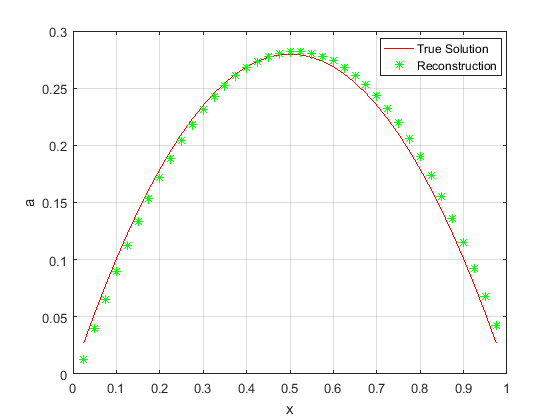
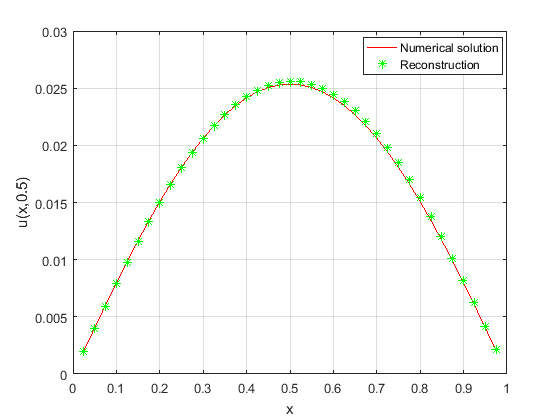
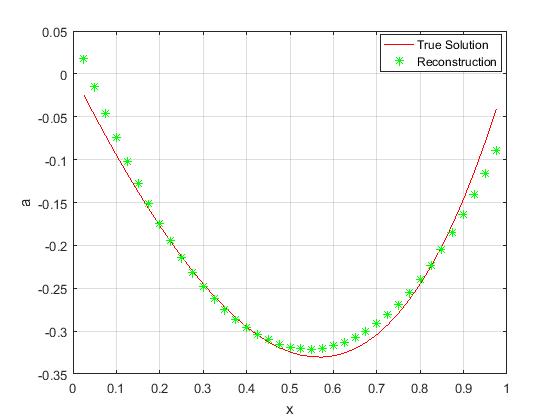
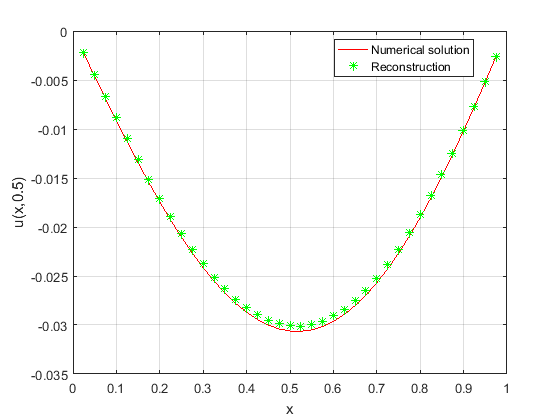
In figure 1-2, for case(a), the iteration steps \(k=786\) is obtained using the Algorithm (4.1) to obtain the reconstructed solution of the initial value, and the relative error of the reconstructed solution and the true solution of the initial value \(err_{a}=4.71\%\), the relative error of the reconstructed solution of the direct problem obtained by inversion algorithm and the numerical solution obtained by difference scheme \(err_{u}=1.36\%\). In figure 3-4, for case(b), the iteration steps \(k=863\) and the relative error between the reconstructed solution and the true solution of the initial value \(err_{a}=4.36\%\), the relative error of the numerical solution and the reconstructed solution of the direct problem \(err_{u}=1.29\%\). In figure 5-6, for case(c), the iteration steps \(k=1016\) and the relative error between the reconstructed solution and the true solution of the initial value \(err_{a}=6.80\%\), the relative error of the numerical solution and the reconstructed solution of the direct problem \(err_{u}=1.77\%\). In figure 7-8, for case(d), owing to the poor regularity of the target function, the reconstruction results are not as well as those of the smooth case in the previous examples. The iteration steps \(k=2217\) and the relative error between the reconstructed solution and the true solution of the initial value \(err_{a}=12.67\%\), the relative error of the numerical solution and the reconstructed solution of the direct problem \(err_{u}=3.56\%\). Figure 1-6 and the relative error \(err_{a}, err_{u}\) indicate the efficiency and accuracy of the proposed Algorithm (4.1) for simulating the unique continuation.

Concluding remarks

In this paper, on the basis of the Theta function method, we first gave a representation formula of the solution and showed the uniqueness of the solution to the Cauchy problem by the use of the Laplace transform argument, from which we further verified the unique continuation property of the solution to (1.1). Specifically, we proved that a solution to a fractional diffusion equation can be uniquely determined from an interior subdomain. The method used in the proof is new method that can effectively overcome the difficulties caused by the non-locality of fractional derivatives. This result and the used methods not only provide theoretical foundation for the fractional diffusion equations but also open up new possibilities for studying related inverse problems in areas such as inverse source problems and approximate control problem in practical applications.

Let us mention that the proof of the unique continuation principle heavily relies on the Theta function method which enables one to derive an explicit representation formula of the solution. It would be interesting to investigate what happens about the unique continuation property of the solution in the general dimensional case. Moreover, in Theorem 1, we only proved the uniqueness result for determining the solution from the information of the solution in interior domain. In comparison, it is known that conditional stability results hold for the same problems for elliptic or parabolic equations based on Carleman estimates. Unfortunately, such techniques do not work in the case of fractional diffusion equations due to the absence of the fundamental integration by parts for the fractional derivatives.

In the numerical aspect, we reformulate the unique continuation principle as an optimization problem with Tikhonov regularization. After the derivation of the corresponding variational equation, we can characterize the minimizer by employing the associated backward fractional diffusion equation, which results in our iterative method. Then several numerical experiments for the reconstructions are implemented to show the efficiency and accuracy of the proposed Algorithm 4.1 for simulating the unique continuation. Here we point out that the homogeneous boundary condition was assumed in deriving Algorithm 4.1. It will be intriguing to derive Algorithm 4.1 without assuming the homogeneous boundary condition, as the algorithm for the general case still remains a challenge to be solved.

Acknowledgment

This second author was supported by National Natural Science Foundation of China No. 12271277. This work was partly supported by the Open Research Fund of Key Laboratory of Nonlinear Analysis & Applications (Central China Normal University), Ministry of Education, P. R. China.

Conflict of interest:

The authors declare no conflict of interest.

References

1. Adams, E.E., and Gelhar, L.W. (1992). Field study of dispersion in a heterogeneous aquifer: 2. Spatial moments analysis. Water Resour. Res. 28: 3293–307.View

2. Cannon, J. (1984). The One-Dimensional Heat Equation, Encyclopedia of Mathematics and Application. Addison-Wesley, Menlo Park, CA, View

3. Cheng, J., Lin, C-L., and Nakamura, G. (2013). Unique continuation property for the anomalous diffusion and its application. J. Differential Equations, 254: 3715–28.View

4. Doss, R. (1988). An elementary proof of Titchmarsh¨s convolution theorem. Proceedings of the American Mathematical Society, 104(1): 181–184.View

5. Fujishiro, K., and Yamamoto, M. (2014). Approximate controllability for fractional diffusion equations by interior control. Appl. Anal. 93(9): 1793–1810.View

6. Hatano Y, Hatano N. (1998). Dispersive transport of ions in column experiments: An explanation of long-tailed profiles. Water Resources Research, 34(5): 1027–33.View

7. Jiang, D., Li, Z., Liu, Y. and Yamamoto, M. (2017). Weak unique continuation property and a related inverse source problem for time-fractional diffusion-advection equations. Inverse Problems, 33(5): 055013.View

8. Eidelman, S.D., Kochubei, A.N. (2004). Cauchy problem for fractional diffusion equations. Journal of Differential Equations, 199(2): 211–255.View

9. Li, Z., Liu, Y. and Yamamoto, M. (2015). Initial-boundary value problems for multi-term timefractional diffusion equations with positive constant coefficients. Applied Mathematics and Computation, 257: 381–397.View

10. Li, Z., Yamamoto, M. (2018). Unique continuation principle for the one-dimensional timefractional diffusion equation. Fractional Calculus and Applied Analysis, 22(3): 644–657.View

11. Lin, C-L., and Nakamura, G. (2016). Unique continuation property for anomalous slow diffusion equation. Commun. Partial Diff. Eqns, 41(5): 749–758.View

12. Liu Y. (2027). Strong maximum principle for multi-term time-fractional diffusion equations and its application to an inverse source problem. Comput. Math. Appl. 73(1): 96-108.View

13. Liu, Y., Hu, G. and Yamamoto, M. (2021). Inverse moving source problems for time-fractional evolution equations: determination of profiles. Inverse Probl. 37(8): 084001 (23pp).View

14. Liu, Y., Rundell, W., Yamamoto, M. (2016). Strong maximum principle for fractional diffusion equations and an application to an inverse source problem. Frac. Calc. Appl. Anal. 19(4): 888–906.View

15. Luchko Y. (2010). Some uniqueness and existence results for the initial-boundary-value problems for the generalized time-fractional diffusion equation. Comput. Math. Appl. 59(5): 1766–1772..View

16. Luchko Y. (2011). Initial-boundary-value problems for the generalized multi-term timefractional diffusion equation. J. Math. Anal. Appl. 374(2): 538–48.View

17. Podlubny I. (1999). Fractional Differential Equations (San Diego: Academic)View

18. Rundell, W., Xu, X., and Zuo, L. (2013). The determination of an unknown boundary condition in a fractional diffusion equation. Applicable Analysis, 92(7): 1511–1526.View

19. Sakamoto, K., and Yamamoto, M. (2011). Initial value/boundary value problems for fractional diffusion-wave equations and applications to some inverse problems. J. Math. Anal. Appl. 382: 426–447.View

20. Sun, C., Liu, J. (2020). Reconstruction of the space-dependent source from partial Neumann data for slow diffusion system. Acta Math. Appl. Engl. Ser. 36: 166–182.View

21. Titchmarsh, E.C. (1926). The zeros of certain integral functions. Proceedings of the London Mathematical Society, s2-25 (1): 283–302.View

22. Schiff, J.L. (2013). The Laplace Transform: Theory and Applications. Springer Science & Business Media.View