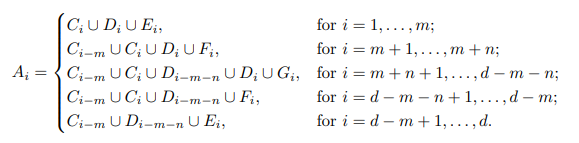Journal of Comprehensive Pure and Applied Mathematics Volume 3 (2025), Article ID: JCPAM-114
https://doi.org/10.33790/cpam1100114Research Article
On Complete Positivity of Sparse Symmetric Toeplitz Matrices
Siyang Tao
Department of Mathematical Sciences, Ball State University, Muncie, IN, USA.
Corresponding Author: Siyang Tao, Department of Mathematical Sciences, Ball State University, Muncie, IN, USA.
Received date: 20th December, 2024
Accepted date: 06th January, 2025
Published date: 08th January, 2025
Citation: Tao, S. (2025). On Complete Positivity of Sparse Symmetric Toeplitz Matrices. J Comp Pure Appl Math, 3(1):1-09. doi: https://doi.org/10.33790/cpam1100114.
Copyright: ©2025, This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited
Abstract
Completely positive matrices play a central role in optimization and mathematical modeling, particularly in reformulating NP-hard problems as linear programs over convex cones. This paper investigates the complete positivity of symmetric Toeplitz matrices with two nonzero coefficients, a sparse and structured class of matrices. By exploring their connection to Bernoulli-compatible matrices, we derive novel sufficient conditions for their complete positivity and extend these results to specific probabilistic and optimization frameworks. The findings deepen our understanding of structured matrices and enhance their applicability in stochastic modeling, control theory, and signal processing. Additionally, we provide illustrative examples and practical implications for these conditions, contributing to both theoretical advancements and computational feasibility in matrix analysis.
Introduction
Completely Positive Matrices (CPMs) hold a central position in mathematical research, connecting various fields ranging from operator theory and harmonic analysis to their practical applications in computer vision and signal processing. These matrices not only deepen our comprehension of positive semidefinite matrices but also provide valuable insights into numerous areas of mathematics and engineering. Notably, in the realm of optimization, a substantial number of NP-hard optimization problems defined over convex cones can be reformulated as linear optimization problems over the cone of completely positive matrices, see [2, 5, 8, 11, 15]
A CPM is a real \(d \times d\) square matrix \(\mathbf{A}\) that admits a factorization \[\mathbf{A}=\mathbf{B}\mathbf{B}^\mathsf{T},\] where \(\mathbf{B}\) is an \(d \times m\) matrix with nonnegative elements. This factorization highlights the intrinsic positive semidefinite and symmetry aspects of such matrices. We denote the set of all \(d \times d\) completely positive matrices by \(\mathcal{C}_d\). Although determining complete positivity is NP-hard (see ), we identify some subsets of \(\mathcal{C}_d\) that can be easily determined.
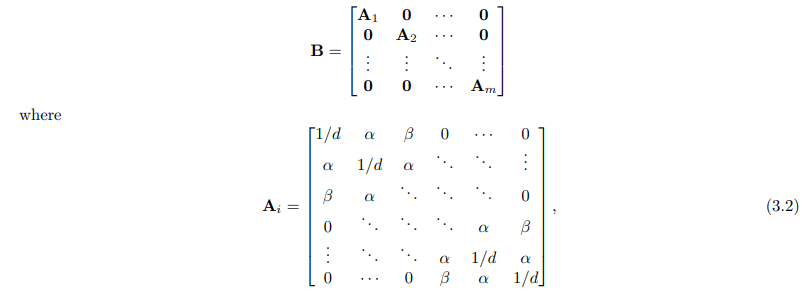
This paper focuses on symmetric Toeplitz matrices, a special class of matrices where each descending diagonal from left to right is constant, as described by: \[\begin{bmatrix} \alpha_0 & \alpha_1 & \alpha_2 & \cdots & \alpha_{d-2} & \alpha_{d-1} \\ \alpha_1 & \alpha_0 & \alpha_1 & \ddots & & \alpha_{d-2} \\ \alpha_2 & \alpha_1 & \ddots & \ddots & \ddots& \vdots \\ \vdots & \ddots &\ddots & \ddots & \alpha_1 &\alpha_2 \\ \alpha_{d-2} & &\ddots & \alpha_1 & \alpha_0 & \alpha_1\\ \alpha_{d-1} & \alpha_{d-2} & \cdots &\alpha_2 & \alpha_1 & \alpha_0 \end{bmatrix}, \label{Toep_matrix}------(1.1)\] where \(\alpha_i \geq 0\), for \(i=0,\ldots,d-1\). Complete positivity is vital in the realm of Toeplitz matrices, enhancing our theoretical understanding of these matrices and bolstering their practical utility. This property ensures positive semidefiniteness, making Toeplitz matrices, especially the positive semidefinite ones, essential in engineering fields such as stochastic filtering (), digital signal processing ( and ), and control theory (). For an in-depth examination of the subject, please refer to the comprehensive review provided in .
Our motivation stems from the need to understand the structure and properties of these matrices, particularly their role in extreme value theory, where Bernoulli compatible matrices are a significant concept. We delve into the question of when a symmetric Toeplitz matrix can be a Bernoulli compatible matrix and extend this inquiry to the realm of complete positivity.
A similar direction but different focuses is the work in which is centered on investigating the complete positivity of matrices characterized by particular sparsity patterns, including acyclic or circular matrices. It demonstrates that in such instances, the verification of complete positivity and the determination of factorizations can be achieved in linear time. For further related studies, readers are directed to the references contained therein.
The paper is organized as follows: Section 2 revisits the concept of Bernoulli compatible matrices, pivotal in extreme value theory. In Section 3, we present a sufficient condition for symmetric Toeplitz matrices with two non-zero coefficients to qualify as Bernoulli compatible matrices and explore their extension to complete positivity.
Throughout, we adhere to the convention of representing vectors and matrices in boldface, with \(a_{ij}\), denoting the element in the \(i\)-th row and \(j\)-th column of a matrix \(\mathbf{A}\). The vectors and matrices with all elements equal to \(0\) and \(1\) are denoted by \(\mathbf{0}\) and \(\mathbf{J}\), respectively. Our standard probability space is denoted by \(([0,1],\mathcal{L},\lambda)\), where \(\mathcal{L}\) consists of the Lebesgue measurable subsets within the interval \([0,1]\), and \(\lambda\) is the Lebesgue measure defined on \([0,1]\). The ceiling function is denoted by \(\lceil \cdot \rceil\).
An overview of Bernoulli compatible matrices
In this section, we explore the intricacies of Bernoulli compatible matrices (BCMs). These matrices serve as a crucial bridge between discrete random processes and matrix theory, thereby playing an indispensable role in a wide range of mathematical and statistical applications.
A matrix \(\mathbf{B}\) of size \(d \times d\) is classified as a Bernoulli compatible matrix if it can be represented as \(\mathbb{E}{\left(\mathbf{X}\mathbf{X}^{\mathsf{T}}\right)}\), where \(\mathbf{X}\) is a \(d\times 1\) random vector taking values in \(\{0,1\}^d\). The set of all such matrices is denoted by \(\mathcal{B}_{d}\). Notably, the matrix \(\mathbb{E}{\left(\mathbf{X}\mathbf{X}^{\mathsf{T}}\right)}\) forms a convex combination of points in the set: \[\label{eqn_vertices} \left\{\mathbf{x}\mathbf{x}^\mathsf{T}: \mathbf{x}\in \{0,1\}^d\right\},------(2.1)\] implying that \(\mathcal{B}_d\) is the convex hull of these points, a closed convex set. In contrast, \(\mathcal{C}_d\) represents the convex cone with extreme directions formed by \(\left\{\mathbf{x}\mathbf{x}^\mathsf{T}: \mathbf{x}\in [0,1]^d\right\}\) (see Section 2.2 of ). It is important to note that \(\mathcal{B}_{d} \subseteq \mathcal{C}_d\), and this assertion is substantiated by Corollary 2.3 in , which states:
Proposition 2.1. Any Bernoulli compatible matrix is completely positive.
Consider a matrix \(\mathbf{B}\in\mathcal{B}_d\), associated with a random vector \(\mathbf{X}=(X_1,\ldots,X_d)^\mathsf{T}\) taking values in \(\{0,1\}^d\) such that \(\mathbf{B}=\mathbb{E}{\left(\mathbf{X}\mathbf{X}^\mathsf{T}\right)}\). Defining events \(A_i:=\{X_i=1\}\), for \(i=1,\ldots,d\), the matrix \(\mathbf{B}\) can be expressed as: \[\begin{aligned} \label{BCprob} \mathbf{B}=\begin{bmatrix} {\rm Pr}\left(A_1\right) & {\rm Pr}\left(A_1\cap A_2\right) & \cdots & {\rm Pr}\left(A_1\cap A_d\right) \\ {\rm Pr}\left(A_1\cap A_2\right) & {\rm Pr}\left(A_2\right) & \cdots & {\rm Pr}\left(A_2\cap A_d\right) \\ \vdots & \vdots & \ddots & \vdots \\ {\rm Pr}\left(A_1\cap A_d\right) & {\rm Pr}\left(A_2\cap A_d\right) & \cdots & {\rm Pr}\left(A_d\right) \\ \end{bmatrix}. \end{aligned}------(2.2)\]
This leads us to inquire whether a matrix’s membership in \(\mathcal{B}_d\) can be determined by the existence of events \(A_i\) in a probability space, such that their probabilities and those of their binary intersections correspond to the matrix’s entries. This query is affirmatively addressed in Corollary 3 of :
Proposition 2.2. A \(d \times d\) matrix \(\mathbf{B}\) is a BCM if and only if there exist events \(A_i\), \(i=1,\ldots, d\), on a probability space such that the matrix \(\mathbf{B}\), as defined in (2.2), is equal to \(\mathbf{B}\).
This proposition forms a cornerstone of our analysis in the subsequent section, where we explore the conditions under which a given matrix can be classified as a BCM.
Symmetric Toeplitz matrices with two non-zero \(\alpha_i\)s
In this section, we explore special cases of symmetric Toeplitz matrices. Building upon the work of , which provides sufficient and necessary conditions for 1- and 2-dependent matrices (where only \(\alpha_1\) is positive and only both \(\alpha_1\) and \(\alpha_2\) are positive, respectively), we extend these results to consider the cases where any two \(\alpha_i\)s are positive. This extension enables a deeper understanding of the structural nuances of symmetric Toeplitz matrices in specific sparse configurations.
We recall that \(\mathcal{C}_d\) represents a convex cone, a fact that leads to an immediate and important implication for completely positive matrices, as stated in the following proposition:
Proposition 3.1. Let \(\mathbf{B}\) be any completely positive matrix. Then \(k\mathbf{B}\) is completely positive for any \(k \geq 0\).
Interestingly, this property allows us to focus on symmetric Toeplitz matrices with diagonal elements normalized to \(\alpha_0:= 1/d\). This representation aligns with the probability space framework and sets the stage for the ensuing analysis.
We now consider symmetric Toeplitz matrices where two of the \(\alpha_i\) values, denoted as \(\alpha_m = \alpha\) and \(\alpha_{m+n}=\beta\), for \(m=1,\ldots,d-2\), and \(n=1,\ldots,d-m-1\), are positive, while all other \(\alpha_i\) values are zero. In this case, the matrix takes the form:
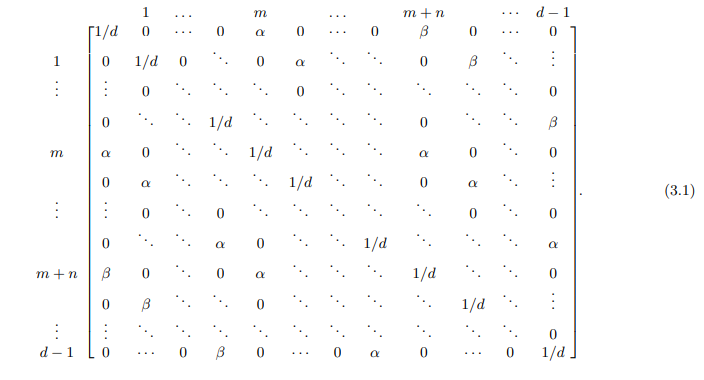
It’s important to note that in this layout, the indices i, as indicated by the column on the left and the row above the matrix, correspond to the (i + 1)-th column and row of the matrix.
Theorem 3.2. A \(d \times d\) symmetric Toeplitz matrix with \(1/d\) main diagonal elements and positive elements on the \(m\)- and \((m+n)\)-diagonal, as specified in (3.1), is in \(\mathcal{B}_d\) if and only if the following conditions are satisfied:
For \(m=n\), the conditions vary as follows:
For \(5m+1 \leq d\), \(\alpha, \beta\geq 0; \; \alpha+4\beta \leq 2/d; \; 2\alpha-\beta \leq 1/d\); For \(4m+1 \leq d < 5m+1\), \(2\alpha-\beta \leq 1/d\); For \(3m+1 \leq d < 4m+1\), \(\alpha, \beta\geq 0; \; \alpha + \beta \leq 1/d; \; 2\alpha-\beta \leq 1/d\); For \(2m+1 \leq d < 3m+1\), \(\alpha\geq 0; \; 0 \leq \beta \leq 1/d; \; 2\alpha-\beta \leq 1/d\). For \(m \neq n\), the conditions vary as follows:
For \(2m+2n+1 \leq d\), \(\alpha, \beta\geq 0;\) \(2\alpha+2\beta \leq 1/d\); For \(2m+n+1 \leq d < 2m+2n+1\), \(\alpha, \beta\geq 0;\) \(2\alpha+\beta \leq 1/d\); For \(m+n+1 \leq d < 2m+n+1\), \(\alpha, \beta\geq 0;\) \(\alpha+\beta \leq 1/d\).
Proof: For Case 1, when m = n, by permuting the rows and columns of (3.1), we can obtain the following block diagonal matrix B, where each block is a two-dependent matrix:
is a ki * ki matrix incorporating the i, i + m, . . . , i + (ki − 1)m-th rows and columns of (3.1) with ki= [(d − i + 1)/m], for i = 1, . . . , m. Note that a matrix of the form (3.1) is in Bd if and only if B is in Bd (see Lemma 12 in [17]).
Now, let’s consider the subcase 5m + 1 ≤ d (or equivalently, k1 ≥ 6). For the only if part, if B is in Bd, then Ai must be in Bki , for i = 1, . . . , m, respectively. The necessary and sufficient condition for A1 to be in Bk1 is given in Proposition 21 of [17], which is α,β≥0; α+4β≤2/d; 2α-β≤1/d. Note that Ai , for i = 2, . . . , m, either equals A1 or has one dimension less, then the conditions ensuring that Ai is in Bki , for i = 2, . . . , m is identical or less stringent to the previous conditions (see Remark 22 of [17]). This completes the proof for this subcase. For the if part, given α and β satisfy these conditions, then A1 is in Bk1. If ki ≥6, the conditions for α and β remain the same, implying that Ai is in Bki. If ki = 5, the constraints on α and β are less restrictive than for ki = 6 (see Remark 22 of [17]), confirming Ai is in Bki . Therefore, Ai is in Bki , for i = 1, . . . , m, which implies that B∈Bd.
The following three subcases of Case 1 are equivalent to that of k1 = 5, 4, and 3, respectively. Using a similar argument as above, we can conclude that B in Bd if and only if A1 in Bk1 . Again, the necessary and sufficient conditions for A1 in Bk1 are given in Remark 22 of [17]. We observe that 2m + 1 ≥ d, and this completes the proof of Case 1.
For Case 2, where m ≠ n, unlike case 1, there are no 3 × 3 principal submatrices of B where all of its off-diagonal elements are positive. We consider the first subcase, where 2m+ 2n+ 1 ≥ d. To prove the only if part, suppose B is in Bd. Let the sets Ai , for i = 1, . . . , d, be those corresponding to B as specified in (3.1).
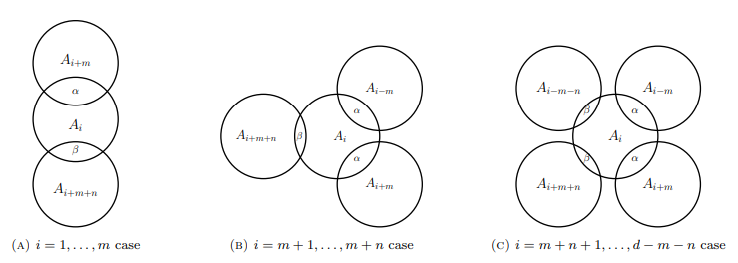
It is easy to see that Ai , for i = 1, . . . , d, intersect with two, three, or four sets according to the following five patterns:
Note that the last two patterns are similar to that of the first two patterns, respectively, so we can only focus on the first three. The Venn diagrams illustrating the sets Ai , for i = 1, . . . , d − m − n, are shown in Figure 1. By imposing the non-negativity constraint on the probability of each set and the constraint that Pr (Ai) = 1/d, for i = 1, . . . , d, we obtain the following inequalities:
α,β≥0; ------(3.3)
α+β≤1/d;------(3.4)
2α+β≤1/d;------(3.5)
2α+2β≤1/d;------(3.6)
These constraints become more restrictive from (3.4) to (3.6). This completes the proof for the only if part in the first subcase. Similar arguments can be made for the second subcase 2m+n+1≤d < 2m+2n+1 and the third subcase m+n+ 1 ≤ d < 2m+n+ 1. In the second subcase, the constraints remain (3.3)-(3.5), and in the third subcase, the constraints remain (3.3) and (3.4). Observing that d ≥ m + n + 1, these completes the proof for the only if part in all subcases.
For the if part, let us initially focus on the first subcase. We will show that the matrix B = (bij ) takes the form of (3.1), for α,β satisfying 2α+2β≤1/d, belongs to Bd, for any 2m + 2n + 1 ≤ d. To validate this, we need to establish the existence of events Ai , i = 1, . . . d, on a probability space with identical probabilities of 1/d such that bij = Pr (Ai ∩ Aj ), for 1 ≤ i, j ≤ d. To this end, we construct disjoint sets on a non-atomic probability space. These sets include Ci , for i = 1, . . . d − m, Di , for i = 1, . . . d − m − n, Ei , for i = 1, . . . m, d − m + 1, . . . , d, Fi , for i = m + 1, . . . m + n, d − m − n + 1, . . . , d − m, and Gi , for i = m + n + 1, . . . , d − m − n, with probabilities.
Pr (Ci) = α; Pr (Di) = β; Pr (Ei) = 1/d − α − β
Pr (Fi) = 1/d − 2α − β; and Pr (Gi) = 1/d − 2α − 2β.
Define
We see that Pr (Ai ∩ Aj ) = bij , for 1 ≤ i, j ≤ d, which completes the proof for the first subcase. Similarly, we can construct sets that satisfy the other two cases. □This can be done as the sum of the probabilities of all above-mentioned sets are (d-m)α + (d-m-n)β + 2m(1/d-α-β)+2n(1/d-2α-β)+(d-2m-2n)(1/d-2α-2β)= 1-(d-m)α-(d-m-n)β<1.
Example 3.1. Consider two distinct \(13 \times 13\) matrices, \(\mathbf{B}_1\) and \(\mathbf{B}_2\), defined as follows: \[\mathbf{B}_1=\begin{bmatrix} 1/13&0&0& \alpha &0&0& \beta &0&0&0&0&0&0 \\ 0&1/13&0&0 & \alpha &0&0& \beta &0&0&0&0&0\\ 0&0&1/13&0 & 0 &\alpha &0&0& \beta &0&0&0&0\\ \alpha &0&0&1/13&0 & 0 &\alpha &0&0& \beta &0&0&0\\ 0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0&0& \beta &0&0\\ 0 &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0&0& \beta&0 \\ \beta &0 &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0&0 & \beta\\ 0 &\beta &0 &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0 &0\\ 0 & 0 &\beta &0 &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0 \\ 0 &0 & 0 &\beta &0 &0 &\alpha&0 &0&1/13&0 & 0 & \alpha \\ 0 & 0 &0 & 0 &\beta &0 &0 &\alpha&0 &0&1/13&0 &0\\ 0 &0 & 0 &0 & 0 &\beta &0 &0 &\alpha&0 &0&1/13&0 \\ 0 &0 &0 & 0 &0 & 0 &\beta &0 &0 &\alpha&0 &0&1/13 \\ \end{bmatrix},\] where \(m=n=3\) aligns with the second subcase of Case 1.
\[\mathbf{B}_2=\begin{bmatrix} 1/13&0&0& \alpha &0& \beta &0&0&0&0&0&0 &0 \\ 0&1/13&0&0 & \alpha &0& \beta &0&0&0&0&0 &0\\ 0&0&1/13&0 & 0 &\alpha &0& \beta &0&0&0&0&0\\ \alpha &0&0&1/13&0 & 0 &\alpha &0&\beta &0&0&0&0\\ 0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0& \beta &0&0&0\\ \beta &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0&\beta&0&0 \\ 0 &\beta &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0&\beta&0 \\ 0 &0 &\beta &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0 & \beta\\ 0 & 0 &0 &\beta &0 &\alpha&0 &0&1/13&0 & 0 &\alpha &0 \\ 0 &0 & 0 &0 &\beta &0 &\alpha&0 &0&1/13&0 & 0 & \alpha \\ 0 & 0 &0 & 0 &0 &\beta &0 &\alpha&0 &0&1/13&0 &0 \\ 0 &0 & 0 &0 & 0 &0 &\beta &0 &\alpha&0 &0&1/13 &0 \\ 0 & 0 &0 & 0 &0 & 0 &0 &\beta &0 &\alpha&0 &0&1/13 \\ \end{bmatrix},\] where \(m=3\) and \(n=2\), corresponding to the first subcase of Case 2. By Theorem 3.2, \(\mathbf{B}_1\) is a BCM if and only if \(\alpha\geq 0; \; 0 \leq \beta \leq 1/26; \; \alpha + \beta \leq 1/13; \; 2\alpha-\beta \leq 1/13\), while \(\mathbf{B}_2\) is a BCM if and only if \(\alpha, \beta\geq 0;\) \(2\alpha+2\beta \leq 1/13\).
Remark 3.3. In the special case where \(m=n=1\), the matrix in (3.1) is a two-dependent matrix, meaning only the first two diagonals are positive. The conditions for this case align with those stated in Proposition 21 and Remark 22 of [17], underpinning Case 1.
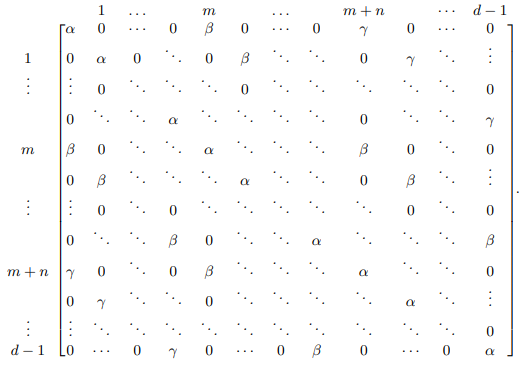
To broaden the application of the specific case outlined in (3.1) towards the complete positivity of general symmetric Toeplitz matrices featuring two non-zero coefficients, we adapt the conditions presented in Theorem 3.2. This adaptation involves the substitution of \(\alpha\) with \(\beta/(d\alpha)\) and \(\beta\) with \(\gamma/(d\alpha)\). By implementing these substitutions, we formulate the following corollary, thereby expanding our analysis to encompass a more extensive array of symmetric Toeplitz matrices:
Corollary 3.4. A \(d \times
d\) symmetric Toeplitz matrix with \(\alpha\) main diagonal elements and
positive elements \(\beta\) and \(\gamma\) only on the \(m\)- and \((m+n)\)-diagonal of the form
is completely positive if the
following conditions are satisfied:
For \(m=n\), the conditions vary as follows:
For \(m \neq n\), the conditions vary as follows:
For \(2m+2n+1 \leq d\), \(\alpha, \beta, \gamma\geq 0;\) \(2\beta+2\gamma \leq \alpha\); For \(2m+n+1 \leq d < 2m+2n+1\), \(\alpha, \beta, \gamma\geq 0;\) \(2\beta+\gamma \leq \alpha\); For \(m+n+1 \leq d < 2m+n+1\), \(\alpha, \beta, \gamma\geq 0;\) \(\beta+\gamma \leq \alpha\).
Remark 3.5. It is well-established that any symmetric, nonnegative, diagonally dominant matrix is completely positive. That is, for a matrix \(\mathbf{A}_{d \times d} = (a_{ij})\), where \(a_{ij} \geq 0\), \(a_{ij} = a_{ji}\), and \[a_{ii} \geq \sum_{k \neq i} a_{ik}, \quad \text{for all } i,\] then \(\mathbf{A}\) belongs to \(\mathcal{C}_d\). However, the matrices discussed in Corollary 3.4 are not necessarily diagonally dominant. For instance, consider the completely positive matrix \(\mathbf{J}_{3 \times 3}\) with \(m=n=1\), which is not diagonally dominant.
<Discussion and Conclusion
Recall that the matrix in (1.1) can be expressed as \(T_d(f)\), where the generating function is given by \[f(\theta):=\alpha_0+2\sum_{i=1}^{d-1}\alpha_i\cos(i\theta),\quad \theta \in [0, \pi],\] see and and the references therein. It is known that if \(f\) is nonnegative on \([0,\pi]\) and not almost surely equal to \(0\), then the Toeplitz matrix \(T_d(f)\) is positive definite for any positive order \(d\) (see Corollary 5.1 of ). Moreover, its eigenvalues can be computed using highly efficient algorithms, even when the coefficients \(\alpha_i\) are complex, see and .
When considering the matrix in (3.1), its generating function specializes to the trigonometric polynomial \[1/d+2\alpha \cos (m\theta)+2 \beta \cos ((m+n)\theta).\] Ensuring that this polynomial remains nonnegative over \([0,\pi]\) guarantees the matrix is positive definite, making it a valuable preliminary check for complete positivity.
This paper primarily examines symmetric Toeplitz matrices and identifies the key conditions under which they are Bernoulli compatible matrices—a classification of particular interest in extreme value theory. We further extend our analysis to the concept of complete positivity, focusing on symmetric Toeplitz matrices in which only two of the \(\alpha_i\) coefficients are nonzero. For these matrices, we establish sufficient conditions that ensure complete positivity. These findings not only improve the computational feasibility of working with such matrices but also open new research directions in the broader domain of Toeplitz matrices and their applications.
Conflict of Interest
There is no conflict of interest.
References
S. Al-Homidan. (2007). Approximate toeplitz matrix problem using semidefinite programming, Journal of optimization theory and applications 135, 583–598.View
L. Bai, J. E. Mitchell, and J.-S. Pang. (2016). On conic qpccs, conic qcqps and completely positive programs, Mathematical Programming 159, 109–136.View
A. Berman and N. Shaked-Monderer. (2003). Completely positive matrices, World Scientific.View
M. Bogoya, S. M. Grudsky, and S. Serra-Capizzano. (2024). Fast non-Hermitian Toeplitz eigenvalue computations, joining matrixless algorithms and FDE approximation matrices,” SIAM Journal on Matrix Analysis and Applications, vol. 45, no. 1, 284–305.View
I. M. Bomze, M. Dur, E. De Klerk, C. Roos, A. J. Quist, and T. Terlaky ¨ . (2000). On copositive programming and standard quadratic optimization problems, Journal of Global Optimization 18, 301–320.View
A. Bottcher and S. M. Grudsky. (2005). Spectral properties of banded Toeplitz matrices. SIAM.View
S. Boyd, L. El Ghaoui, E. Feron, and V. Balakrishnan. (1994).Linear matrix inequalities in system and control theory, SIAM.View
S. Burer. (2009). On the copositive representation of binary and continuous nonconvex quadratic programs, Mathematical Programming 120, 479–495. View
P. J. Dickinson and L. Gijben. (2014). On the computational complexity of membership problems for the completely positive cone and its dual, Computational optimization and applications 57, 403–415.View
P. J. C. Dickinson and M. Dur¨ . (2012). Linear-time complete positivity detection and decomposition of sparse matrices, SIAM Journal on Matrix Analysis and Applications 33, 701–720. View
M. Dur. (2010). Copositive programming–a survey, in Recent Advances in Optimization and its Applications in Engineering: The 14th Belgian-French-German Conference on Optimization, Springer, 3–20. View
S.-E. Ekstrom, C. Garoni, and S. Serra-Capizzano ¨ . (2018). Are the eigenvalues of banded symmetric Toeplitz matrices known in almost closed form?,” Experimental Mathematics, vol. 27, no. 4, 478–487. View
P. Embrechts, M. Hofert, and R. Wang. (2016). Bernoulli and tail-dependence compatibility, Ann. Appl. Probab. 26, 1636–1658. View
C. Garoni and S. Serra-Capizzano. (2017). Generalized locally Toeplitz sequences: theory and applications, vol. 1. Springer View
J.-B. Hiriart-Urruty and A. Seeger. (2010). A variational approach to copositive matrices, SIAM Review 52 593–629. View
T. Kailath. (1974). A view of three decades of linear filtering theory, IEEE Transactions on information theory 20, 146–181. View
N. D. Shyamalkumar and S. Tao. (2020). On tail dependence matrices: The realization problem for parametric families, Extremes 23, 245–285. View
R. Skelton. (1992). The jury test and covariance control, in Proceedings of the Symposium on Fundamentals of DiscreteTime Systems, Chicago, Illinois.
C. W. Therrien. (1992). Discrete random signals and statistical signal processing, Prentice Hall PTR.