Abstract

Let \(S\) be a set of positive integers. We say that \(S\) is a subset-sum-distinct set (briefly, \(S\) is an SSD-set) if for any two finite subsets \(X\), \(Y\) of \(S\), \[\sum_{x\in X} x = \sum_{y \in Y} y \quad \Rightarrow \quad X=Y.\]

For fixed positive integers n and p, we set \[S:=\{1,2,2^2,2^3,\dots\}.\]

We prove a sufficient condition for which S(n, p) is an SSD-set.

Introduction

Let \(S\) be a set of positive integers. We say that \(S\) is a subset-sum-distinct set (briefly, \(S\) is an SSD-set) if for any two finite subsets \(X\), \(Y\) of \(S\), \[\sum_{x\in X} x = \sum_{y \in Y} y \quad \Rightarrow \quad X=Y.\]

One of the most interesting and natural SSD-sets is \[S:=\{1,2,2^2,2^3,\dots\}.\] By the uniqueness of binary expansion, \(S\) is certainly an SSD-set.

Stimulated by Erdös’ open question (), finite dense SSD-sets have been considered by many mathematicians (see [1-6] pp.59–60).

On the other hand, it is one of the hardest problems in computer science to determine whether a given set \(S\) is an SSD-set. The difficulty arises from the fact that we need to consider all subsets of \(S\).

The purpose of this paper is as follows: For fixed positive integers \(n\) and \(p\), we set \[\label{S} S(n,p):=\{1^p,2^p,3^p,\dots,n^p\}.---------(1)\] We prove a sufficient condition for which \(S(n,p)\) is an SSD-set.

Main result

Concerning \(S(n,p)\) in [S], we pose the following:

Problem 1.

1. For a fixed \(n\), find a condition on \(p\) for which \(S(n,p)\) is an SSD-set.

2. As a special case of (i), is it true that if \(S(n,r)\) is an SSD-set for some positive integer \(r\), then is so \(S(n,r+1)\)?

2.1. MotivationThe motivation to consider Problem 1 is as follows. For a Morse function \(f:M\to {\mathbb R}\) on a compact manifold \(M\), we define the fiber product by \[C(f):=\{(u,v) \in M \times M\,\;\vert\,\;f(u)=f(v) \}.\] As explained in [8], it is worthwhile to obtain topological information on \(C(f)\).

As \(f\), we consider Morse functions on \(U(n)\). Here \(U(n)\) denotes the unitary group of degree \(n\) consisting of \(n\times n\) unitary matrices.

Recall from [9] that correspondingly to a choice of real numbers \[0<c_1<c_2<\dots<c_n,\] we obtain the canonical Morse function on \(U(n)\). When a positive integer \(p\) is fixed and \(c_i\) is defined by \(c_i=i^p\) for \(1 \leq i \leq n\), we write the Morse function by \(f_{n,p}\).

We already know the following formula \[\label{oeis} \chi (C(f_{n,p}))=(-1)^n \int_0^1 \prod_{j=1}^n \left( 4 \sin ^2 (\pi j^p x)\right) dx,--------(2)\] where \(\chi (C(f_{n,p}))\) denotes the Euler characteristic of the space \(C(f_{n,p})\).

For special cases, we can simplify (2) by the following:

Lemma 2. The equation \[\label{equa} \chi (C(f_{n,p}))=(-2)^n-----------(3)\] holds if and only if \(S(n,p)\) is an SSD-set. (Note that in this case, the right-hand side of (3) does not depend on \(p\).)

Lemma 2 is the motivation for considering Problem 1.

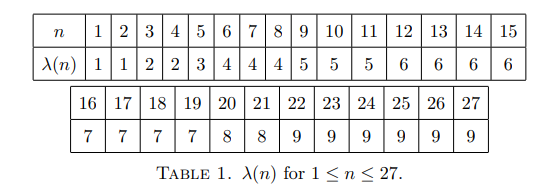
2.2 Example For a fixed \(n\), we set \[\lambda(n):=\min \{p\,\;\vert\,\;\text{$S(n,p)$ is an SSD-set}\}.\] With the aid of a computer, we have the following Table 1.

Remark 3. As Problem 1 (ii) indicates, it is not known whether, for example, \(S(27,p)\) is an SSD-set for all \(p > 9\).

Main result

Now we give an answer to Problem 1.

Theorem 4. If \(p \geq n\), then \(S(n,p)\) is an SSD-set.

Proof of Theorem

We prove Theorem 4 by induction on \(n\).

Base case: Since \(S(1,p)=\{1\}\), Theorem 4 holds for \(n=1\).

Induction step: We assume that \(S(n-1,q)\) is an SSD-set for \(q \geq n-1\). We need to prove that \(S(n,p)\) is an SSD-set for \(p \geq n\). Using the inductive hypothesis, it will suffice to find \(p\) which satisfies \(p \geq n-1\) and the following Condition 5:

Condition 5 (Condition on \(p\)). We require that \(p\) satisfies the following statement: Let \(X\) and \(Y\) be any subsets of \(S(n,p)\) satisfying the following (i) and (ii):

1. \(X \cap Y=\varnothing\), and

2. \(n^p \in Y\).

Then we require that \[\label{sum} \sum_{x\in X} x \not= \sum_{y \in Y} y.\]

In order to find \(p\) which satisfies Condition 5, note that if \(p\) satisfies \[\label{ineq} \sum_{k=1}^{n-1}k^p <n^p,----------(4)\] then \(p\) satisfies Condition 5. We study which \(p\) satisfies (4). Considering the lower Riemann sum, we have \[\label{riem} \sum_{k=1}^{n-1}k^p <\int_1^n x^p \;dx.-------------(5)\] We consider the following inequality: \[\label{ineq2} \int_1^n x^p \;dx<n^p-----------------(6)\] Thanks to (5), if \(p\) satisfies (6), then \(p\) satisfies (4).

We shall prove that if \(p\geq n\), then (6) holds. In fact, \[\int_1^n x^p \;dx=\frac{n^{p+1}-1}{p+1} <\frac{n^{p+1}}{p} \leq \frac{n^{p+1}}{n} =n^p.\] Now we have proved that when \(p\geq n\), (6) holds. Hence (4) also holds. Consequently, Theorem 4 holds.

Conclusions

We show that there are two reasons why our bound \(p\geq n\) in Theorem 4 is far from being the sharp bound. To study concretely, we consider the case \(n=20\). By Table 1, \(S(20,p)\) is an SSD-set when \(p=8\).

The first reason. In order to avoid the difficulty of considering all subsets of \(S(20,p)\), we replace the SSD-condition by (4). More precisely, we have shown that if \(p\) satisfies \[\label{feb} \sum_{k=1}^{19} k^p<20^p,-------------(7)\] then \(S(20,p)\) is an SSD-set. Note that (7) is only a sufficient condition, but far from being the necessary condition for \(S(20,p)\) to be an SSD-set.

The second reason. Direct computations show that (7) holds for \[\label{13} p\geq 13.------------------(8)\] But since the computations are troublesome, we proceeded the argument that if \(p\) satisfies \[\label{feb1} \int_1^{20}x^p\;dx< 20^p,-----------------(9)\] then \(p\) satisfies (7). We obtain from (9) that (7) holds for \[\label{20} p\geq 20.---------------(10)\] Note that (8) and (10) have difference.

Acknowledgments

The author would like to thank the reviewer for carefully reading the manuscript and for valuable comments to improve it.

Conflict of Interest

There is no conflict of interest.

References

1. Bae, J. (1996). On subset-sum-distinct sequences, Analytic Number Theory, Vol. 1, Progr. Math. 138, Birkh¨auser, Boston, 31–37. View

2. Bohman, T. (1996). A sum of packing problem of Erd¨os and the Conway-Guy sequence, Proc. Amer. Math. Soc. 124, 3627–3636. View

3. Conway, J. H., and Guy, R. K. (1969). Solution of a problem of P. Erd¨os, Colloq. Math. 20, 307.

4. Elkies, N. D. (1986). An improved lower bound on the greatest element of a sumdistinct set of fixed order, J. Combin. Theory, Ser. A 41, 89-94. View

5. Erd¨os, P. and Graham, L. (1980). Old and New Problems and Results in Combinatorial Number Theory, Monogr. Enseign. Math., 28, L’Enseignement Math´ematique, Geneva. View

6. Guy, R. K. (1982). Sets of integers whose subsets have distinct sums, Ann. Discrete Math. 12, 141–154. View

7. , (1994). Unsolved Problems in Number Theory, Vol. I of “Unsolved Problems in Intuitive Mathematics”, Springer-Verlag, New York.

8. Kamiyama, Y. (2025). The Euler characteristic of the fiber product of Morse functions, Bull. Korean Math. Soc. 62, 71–80. View

9. Matsumoto, Y. (2002). An Introduction to Morse Theory, Translations of Mathematical Monographs, 208, American Mathematical Society, Providence, RI.